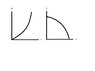Von Neumann
- 101
- 4
Problem:
Which of the wave functions shown might conceivably have physical significance?
Solution:
I have attached a drawing of the two wave functions. According to my book, the one on the right could have physical significance, while the one on the left does not. Can anyone explain why not? They are both single valued, differentiable functions, so I don't see why the left one is apparently disqualified. Thanks for any help.
Which of the wave functions shown might conceivably have physical significance?
Solution:
I have attached a drawing of the two wave functions. According to my book, the one on the right could have physical significance, while the one on the left does not. Can anyone explain why not? They are both single valued, differentiable functions, so I don't see why the left one is apparently disqualified. Thanks for any help.
Attachments
Last edited: