MBBphys
Gold Member
- 55
- 0
Example of a tightrope walker:
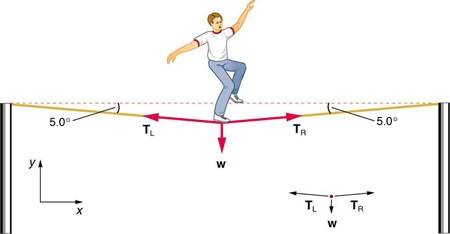
Now, the weight force acts at a point. The rope is stretched. Compressive forces act inwards towards that point (opposite to TL and TR, the tensile forces). The resultant of the compressive forces equals the weight and is in the same direction – the weight force CAUSES the compressive forces.
If the man is stable on the tightrope and not moving, then resultant force is zero.
As string is stretched, tension forces act away from the point where weight acts (see image above). These are labelled TL and TR. The resultant of the tensile forces equals the weight in magnitude, but acts in the opposite direction, producing zero net force.
Is my understanding correct? Thanks in advance for your reply :)
Now, the weight force acts at a point. The rope is stretched. Compressive forces act inwards towards that point (opposite to TL and TR, the tensile forces). The resultant of the compressive forces equals the weight and is in the same direction – the weight force CAUSES the compressive forces.
If the man is stable on the tightrope and not moving, then resultant force is zero.
As string is stretched, tension forces act away from the point where weight acts (see image above). These are labelled TL and TR. The resultant of the tensile forces equals the weight in magnitude, but acts in the opposite direction, producing zero net force.
Is my understanding correct? Thanks in advance for your reply :)