kaycrew22
- 1
- 0
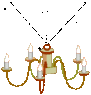
A 28 kg chandelier is suspended 1.5 m below a ceiling by three wires, each of which has the same tension and the same length of 2.0 m (see the drawing attached). Find the tension in each wire.
Equations I believe to be relevant...
W = m * g
Net force Y = T-W
So far I thought:
w = mg
w= 28kg * -9.8 m/s^2
w= 274.4 N
274.4N /3 = 91.47 N
I put this as the answer, but it says I'm wrong. Could someone please explain how this type of question is solved?
Equations I believe to be relevant...
W = m * g
Net force Y = T-W
So far I thought:
w = mg
w= 28kg * -9.8 m/s^2
w= 274.4 N
274.4N /3 = 91.47 N
I put this as the answer, but it says I'm wrong. Could someone please explain how this type of question is solved?