Tension in the hawsers holding a beam

[lendav_rott]

Homework Statement

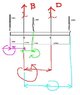
In the illustration we have a beam attached to 2 hawsers which are BX and DY respectively.
We have pressure mounted on different parts of the beam. What is the tension in the hawsers

Homework Equations

The Attempt at a Solution

I don't know how to approach this problem.
Does the pressure in all of these points affect the tension in both of the hawsers? Or pressure in points A and C affect the tension in the hawser BX and pressure in points C and E affect the hawser DY?

 

[mishek]

Same as last time. Draw a FBD. How many unknowns? How many equations do you need?

 

[lendav_rott]

What is an FBD? I haven't studied this in English and abbreviations make it even more difficult :/

Well, the unknowns are the tensions in the hawsers. But before I can even say what the tension is, I must know what affects the tension in either of those hawsers.
This is where I'm stuck - If i stand on one of the ends of the beam, the hawser right next to me will be more tense for sure, but does it apply to the one on the far end?

Or If I stand right in the middle of the distance betweent the 2 hawsers, my weight should affect them equally and as I get closer to one of them, the more I affect the one I m getting closer to and the less will I affect the one I m getting away from - so if my weight were mg, the increase in the tensions of the hawsers should add up.

In this assignment it's as if 3 people are standing on different parts of the beam - well quite heavy for ppl but the idea is the same, but how do each of them affect the whole system? :/

 

[mishek]

What is an FBD? I haven't studied this in English and abbreviations make it even more difficult :/

Sorry, Free Body Diagram.

Well, the unknowns are the tensions in the hawsers. But before I can even say what the tension is, I must know what affects the tension in either of those hawsers.
This is where I'm stuck - If i stand on one of the ends of the beam, the hawser right next to me will be more tense for sure, but does it apply to the one on the far end?

I would say it does, but it is dependent upon lot of things.

Or If I stand right in the middle of the distance betweent the 2 hawsers, my weight should affect them equally and as I get closer to one of them, the more I affect the one I m getting closer to and the less will I affect the one I m getting away from - so if my weight were mg, the increase in the tensions of the hawsers should add up.

In this assignment it's as if 3 people are standing on different parts of the beam - well quite heavy for ppl but the idea is the same, but how do each of them affect the whole system? :/

Draw a free body diagram. Check these photos.

 

[lendav_rott]

Right,

after struggling with the concept for a few days I worked out a solution that overall makes sense to me.

The beam is supported at 2 points, B and D.
Assume the positive direction vertically is toward the floor and horizontally to the right.

The only way the beam will stay this way, is if the total weight is exactly equal to the sum of the tensions.
We have the total Tension B+D and the total weight (7.5+7.5+2.5)kN = 17.5kN
B+D + 17.5 = 0 -> B+D = -17.5kN

Also, the sum of the moments ( I don't know what the word is: the force to cause circular movement around a centerpoint) will also have to be zero if we take either of the hawsers as a centerpoint.
If B is a centerpoint then:
F1 - the total moment to the left of B -> -0.5m * 7.5kN = -3.75kN
F2 - total moment to the right of B -> 0.75m *7.5kN + 1m *7.5kN + 3m *2.5kN + 2.25m *D
2.25m*D is the moment of the other supporting hawser - well it should make sense that we also take the moment of the other hawser into account, otherwise I cannot explain how the beam remains in such a balanced position when clearly there is a lot more moment to the right of B.
so F2 -> 2.25 *D + 13.125kN
F1 = F2 -> 2.25 *D = -16.875kN
and we know that B+D = -17.5kN
So we have 2 unknowns and 2 equations and it should be it.

Have I understood the concept of tension correctly? Is there something else about it? I am fairly confident that I have gone the right way in this assignment.

 

[mishek]

The only way the beam will stay this way, is if the total weight is exactly equal to the sum of the tensions.
We have the total Tension B+D and the total weight (7.5+7.5+2.5)kN = 17.5kN
B+D + 17.5 = 0 -> B+D = -17.5kN

Correct. What does the minus sign means?

If B is a centerpoint then:
F1 - the total moment to the left of B -> -0.5m * 7.5kN = -3.75kN
F2 - total moment to the right of B -> 0.75m *7.5kN + 1m *7.5kN + 3m *2.5kN + 2.25m *D
2.25m*D is the moment of the other supporting hawser - well it should make sense that we also take the moment of the other hawser into account, otherwise I cannot explain how the beam remains in such a balanced position when clearly there is a lot more moment to the right of B.
so F2 -> 2.25 *D + 13.125kN

Your forces on the right cannot have the same moment direction. Please check photo.

 

[lendav_rott]

OH, ofcourse. The moment you painted red, the force is directed upwards not downwards.
So it is:
F1 = -0.5m *7.5kN
F2 = 0.75m *7.5kN + 2.25m *(-D) + 3m *2.5kN
and the rest's simple.

Was that my mistake?

Right and a minor technicality:
-(B+D) = 17.5kN not B+D = -17.5kN
The minus sign means that the tension is directed opposite to the positive direction. I had assumed at the start of the solution that positive is down(vertically)/right(horizontally).

 

[mishek]

OH, ofcourse. The moment you painted red, the force is directed upwards not downwards.

Exactly.

So it is:
F1 = -0.5m *7.5kN
F2 = 0.75m *7.5kN + 2.25m *(-D) + 3m *2.5kN
and the rest's simple.

Was that my mistake?

Yes, I believe that was your mistake. Although, I would like to point out one more thing. The right hand rule I mentioned. The direction of the moment is given by the right hand rule: Counter Clockwise (CCW) is out of the page, Clockwise (CW) is into the page. (I think this is an excellent briefly explained). I myself like to designate the sign of the moment correctly. In your example here, moment from force D is positive and has a z direction (x is right, y is up). That's way I drew those rotations on an attached photo.

Right and a minor technicality:
-(B+D) = 17.5kN not B+D = -17.5kN
The minus sign means that the tension is directed opposite to the positive direction. I had assumed at the start of the solution that positive is down(vertically)/right(horizontally).

Yes, and no. I'll try to explain. When you draw a fbd, then you write equations. For example, for a fbd I attached, I would use following equation:

-A+B-C+D-E=0
B+D=A+C+E
B+D=7.5+7.5+2.5

But if i instead wrote it like this:
A+B+C+D+E=0
B+D=-A-C-E=-17,5

that means that i assumed the wrong direction for some forces (here for A+C+E).

Please sorry if I didn't explain it well.

 

[lendav_rott]

Aah, I understand now, thanks for the explanations, mishek :)