Tension of a particle problem

[Dumbledore211]

Homework Statement

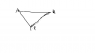
A particle P of mass m is suspended from two strings AP and BP where A and B are attached to 2 points on a horizontal ceiling distance 5l/4 apart as shown in the figure. AP is inelastic and of length l. The modulus of elasticity of BP is λ. Show that the natural length L is given by L= 5λl/3mg+5λ

The Attempt at a Solution

Here the mass attached at the point P is in equilibrium which means that the vertical components of the tension caused in AP and BP nullify the weight acting downward. What I am finding difficult to grasp is the fact that the string AP is inelastic and rigid and how it's rigidity affects the tension since there will be no extension in AP. It would be really helpful if any of you could drop a hint as to how I can establish a relation between the tension of AP and that of BP and if they are equal by any chance?

 

[tiny-tim]

Hi Dumbledore211!

… the vertical components of the tension caused in AP and BP nullify the weight acting downward. What I am finding difficult to grasp is the fact that the string AP is inelastic and rigid and how it's rigidity affects the tension since there will be no extension in AP.

Nearly all strings and cables and beam that you come across will be inelastic, but they still have tension!

Remember that the horizontal components of the tensions will add to zero. ​

 

[Dumbledore211]

@tiny-tim I kind of get what you are trying to put across. Here is how I have approached the problem...
T1= Tension caused in AP
T2= Tension caused in BP
Total Tension, T= T1+T2
Again the horizontal components of the two tensions
T1cosA- T2cosB=0
→ T1cosA=T2cosB
In case of the vertical components of the two tensions
T1sinA + T2sinB=mg
Is it safe to assume that ΔABP is a right-angled triangle?? Since the distance between the point A and B is 5l/4, AP is of length 3l/4 and BP is of length l. We can also assume that angle A=60degrees, B=30degrees and P=90degrees. Is my approach correct?

 

[Dumbledore211]

Okay, I have solved the problem. So, here it goes...
Since ΔABP is a right angled triangle so cos A= 3l/4X 4/5l = 3/5 and likewise cos B=4/5
So 3T1/5= 4T2/5
→ T1=4T2/3
Again for the vertical components sin A= 4/5 and sin B= 3/5
4T1/5 + 3T2/5=mg
→ 4T1 + 3T2= 5mg
→ 16T2 + 9T2/3=5mg
→ 25T2/3=5mg
→5T2=3mg
T2= Tension caused in BP
Here extension in BP is x= l-L
T2= λ(l-L)/L
→ 5(l-L)λ/L=3mg
→ 5λl-5λL=3mgL
→ 3mgL+5λL=5λl
→L=5λl/3mg+5λ

 

[tiny-tim]

@tiny-tim I kind of get what you are trying to put across. Here is how I have approached the problem...
T1= Tension caused in AP
T2= Tension caused in BP
Total Tension, T= T1+T2
Again the horizontal components of the two tensions
T1cosA- T2cosB=0
→ T1cosA=T2cosB
In case of the vertical components of the two tensions
T1sinA + T2sinB=mg

excellent

(except, i would omit "Total Tension, T= T1+T2" …

it isn't necessary, and you're using T1 and T2 to mean vectors even though everywhere else they're just numbers)

Is it safe to assume that ΔABP is a right-angled triangle?? Since the distance between the point A and B is 5l/4, AP is of length 3l/4 …

hold it! where does that come from (3l/4)? it's not in the question or the diagram

 

[Dumbledore211]

@Tiny-tim Actually, I forgot to include the crucial piece of information which is the length of AP. In my M3 book the length of AP has been given as 3l/4. With this missing piece the solution to the whole problem just works out perfectly. Thank you Tiny-tim. Your help is greatly appreciated.