MrMuscle
- 12
- 1
- TL;DR
- Hello, is there an operational order between tensor and matrix multiplications?
Hello, I am calculating the krauss operators to find the new density matrix after the interaction between environment and the qubit.
My question is: Is there an operational order between matrix multiplication and tensor product? Because apparently author is first applying I on |0> and X on |0> and obtain
I|0> =|0>, and X|0>=|1>. instead of first calculating U.
Then instead of making the tensor product he is distributing <0| .
Can someone please explain me why that's the case?
On attachment you can find more detailed explanation.
Thanks in advance!
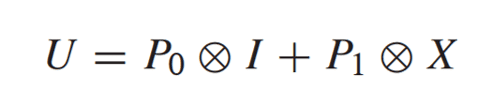
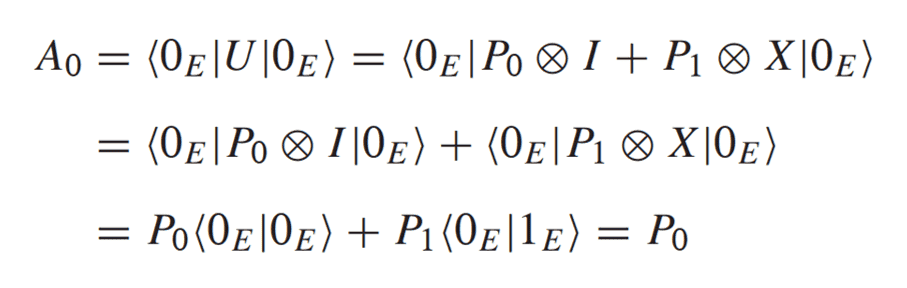
My question is: Is there an operational order between matrix multiplication and tensor product? Because apparently author is first applying I on |0> and X on |0> and obtain
I|0> =|0>, and X|0>=|1>. instead of first calculating U.
Then instead of making the tensor product he is distributing <0| .
Can someone please explain me why that's the case?
On attachment you can find more detailed explanation.
Thanks in advance!
Attachments
Last edited:

