Ibix said:
The equivalence principle only applies locally, so local measurements made by a hovering observer will show what you expect. However, the deflection of star light is not a local effect - the light has traveled in from infinity, passed near the Sun, and climbed back up to Earth. So you should not expect equivalence principle based arguments to work.
The simplifications you make to the Einstein field equations in order to recover Newtonian gravity involve neglecting what you might call spatial curvature, keeping only the time-time equation. So, roughly speaking, the solution is that local measurements will measure a tiny "Newtonian" deflection, but if you simply add them together you neglect the spatial curvature. A line of little labs along the light path won't quite fit together the way Euclid says they would - and that failure to fit together is the extra half of the deflection.
Thank you. I think I have come to a satisfactory understanding of the issue now.
Firstly I don't think it is quite true to imply that the spatial effect is global which the temporal (EP) effect is local.
All physical effects are local and the bending of light in any region of space near a gravitating mass is solely determined by the nature of space-time in the locality. As John Wheeler put it - matter tells space-time how to curve
in the locality, space-time tells matter how to move
in the locality (my additions). My mistake was to think that at a sufficient distance from a mass, the gravitational field would become effectively uniform. This is not the case.
It is clear to me now that the temporal bending is due to the slowing down of light (as seen by an external comoving observer) at points lower down in the potential well, an effect which it is easy to show is equal to
g/c in agreement with the EP. The spatial component of the bending in any locality is due to the non-uniform nature of the field in the locality and I strongly suspect that it is equal (or proportional to) ##\sqrt{dg/dr}## . If this is true than, while
g falls off as an inverse square, the spatial effect will fall off more slowly so at great distances the spatial effect will, in fact dominate, not the temporal one.
Regardless of whether my hunch is correct or not, it remains true that the bending of light in a local region near a spherically symmetrical mass will always require both effects to be taken into account. By considering a strictly uniform gravitational field, in which
dg/dr = 0 the spatial component has been removed.
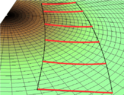
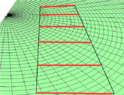
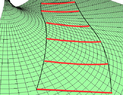
My suggestion about Flamm's paraboloid was dismissed by one contributor but I think he mistook the diagram for a potential well. In fact I believe that Flamm's paraboloid (which as you know is a surface whose metric is the same as the spatial component of the Schwartzchild metric) can be used to provide a legitimate (qualitative) explanation of the bending of light, particularly if the paraboloid is inverted so that there can be no confusion with the more familiar potential well diagram.
Essentially the idea is that the temporal component of the bending is due to the fact that light passing near the star travels more slowly (just like sound waves traveling over water or light waves in a graded index optical fibre); the spatial component is due to the fact that radial distances are 'stretched' closer to the star and therefore light which passes close to the star has further to travel. In traveling from a point A on one side of the star to a point B on the other, a light ray chooses the path with the shortest travel time. (The contributor who mentioned that in GR a geodesic maximises the proper time was confusing proper time with elapsed time. In any case the proper time of a light ray is always zero whichever way it travels.)
The attached diagrams should illustrate the way in which I shall in future explain to my students why the bending of starlight is twice the bending predicted by Newton and the EP.
(BTW Please do not think I am directing these comments at you, Ibix, as I am sure your understanding of GR is much better than mine. I have explained my ideas at length in the hope that other readers of this post will gain a better understanding.)