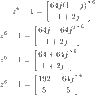You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
The distinct roots of complex number
- Thread starter timeforchg
- Start date
-
- Tags
- Complex Complex number Roots
AI Thread Summary
The discussion revolves around finding the roots of the equation z^6 - 1 = C, where C is a complex number. Participants suggest various methods, including expressing complex numbers in polar form and multiplying out polynomials to solve for real and imaginary parts. There is a focus on simplifying the problem by equating the real and imaginary components of the complex numbers involved. The conversation highlights the challenges of handling complex roots and the importance of strategy in approaching such problems. Ultimately, the original poster expresses gratitude for the assistance received in solving the equation.
Physics news on Phys.org
Simon Bridge
Science Advisor
Homework Helper
- 17,871
- 1,661
Welcome to PF;
is it that z=x+iy: z6-1=c6 (c=a+ib): a,b,x,y are real, a,b are constants?
so you need to find:
(x+iy)^6-(a+ib)^6-1=0
You could multiply out the polynomials and then solve for the real and imaginary parts ... or express each of the complex numbers as exponentials. Which have you tried?
is it that z=x+iy: z6-1=c6 (c=a+ib): a,b,x,y are real, a,b are constants?
so you need to find:
(x+iy)^6-(a+ib)^6-1=0
You could multiply out the polynomials and then solve for the real and imaginary parts ... or express each of the complex numbers as exponentials. Which have you tried?
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
Here's your image, below.timeforchg said:I am trying to find the z0 to z6 roots of this equation but I am stuck here. Anyone care to show the step by step on how to proceed?
Homework Statement
Homework Equations
The Attempt at a Solution
It can be easier to take the power of a complex number when it's expressed in "polar" form.
Assuming your last line is correct:
\displaystyle \frac{192}{5}-j\frac{64}{5}=\frac{64\sqrt{10}}{5}e^{-j\,\tan^{-1}(1/3)}
timeforchg
- 18
- 0
Hi SammyS,
How do you derive to that equation?
How do you derive to that equation?
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
That's polar form for a complex number. (By the Way, I'm not too sure it will be all that helpful here, what with the -1 part of the z6 - 1, and with the arctan in the exponent.)timeforchg said:Hi SammyS,
How do you derive to that equation?
In general, you can express the complex number, a + b j as
<br />
a+bj=\sqrt{a^2+b^2\ }\left(\cos(\theta)+j\sin(\theta)\, \right)\,,
where \displaystyle \tan(\theta)=\frac{b}{a}\ .
Using Taylor series, it can be shown that \displaystyle e^{j\,\theta}=\cos(\theta)+j\sin(\theta)\ .
\displaystyle \cos(\theta)+j\sin(\theta) is also called the cis() function, but the exponential form makes it very handy for taking a complex number to a power.
\displaystyle \frac{192}{5}-j\frac{64}{5}=\frac{64}{5}\left(3-1j\right)where \displaystyle \tan(\theta)=\frac{b}{a}\ .
Using Taylor series, it can be shown that \displaystyle e^{j\,\theta}=\cos(\theta)+j\sin(\theta)\ .
\displaystyle \cos(\theta)+j\sin(\theta) is also called the cis() function, but the exponential form makes it very handy for taking a complex number to a power.
\displaystyle 3-j=\sqrt{3^2+1^2}\left(\cos(\theta)+j\sin(\theta) \right)\,,\ \text{ where }\theta=\arctan\left(\frac{-1}{\ 3}\right)\
\displaystyle =\sqrt{10}\,e^{\,j\,\arctan(-1/3)} \ .
Simon Bridge
Science Advisor
Homework Helper
- 17,871
- 1,661
caveat: you have to be real careful with the signs inside the arctangent. ##\arctan(\frac{-1}{2}) = \pi + \arctan(\frac{1}{-2})##
(arctan is not a good description of the calculation - what you want is the "argument" of the complex number)
If you have a complex number z, then it can be expressed as
$$z = a+jb=|z|e^{j\arg(z)}$$ ... and you know how to find the modulus and argument of a complex number?
So if z is a ratio of powers of complex numbers, eg. $$z=\frac{x^m}{y^n}$$ then you can write: $$z=\frac{(|x|e^{j\arg(x)})^m}{(|y|e^{j\arg(y)})^n }=\frac{|x|^m e^{jm\arg(x)}}{|y|^n e^{jn\arg(y)} } = \frac{|x|^m}{|y|^n} e^{\left [ j(m\arg(x)-n\arg(y)) \right ]} = Ae^{j\theta} = A\cos(\theta) + jA\sin(\theta)$$
(arctan is not a good description of the calculation - what you want is the "argument" of the complex number)
If you have a complex number z, then it can be expressed as
$$z = a+jb=|z|e^{j\arg(z)}$$ ... and you know how to find the modulus and argument of a complex number?
So if z is a ratio of powers of complex numbers, eg. $$z=\frac{x^m}{y^n}$$ then you can write: $$z=\frac{(|x|e^{j\arg(x)})^m}{(|y|e^{j\arg(y)})^n }=\frac{|x|^m e^{jm\arg(x)}}{|y|^n e^{jn\arg(y)} } = \frac{|x|^m}{|y|^n} e^{\left [ j(m\arg(x)-n\arg(y)) \right ]} = Ae^{j\theta} = A\cos(\theta) + jA\sin(\theta)$$
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
I'll try to get to it soon.timeforchg said:Thanks Simon for the warning.
Hey Sammys. I have work out and this is what I came out with.. it looks messy but how do I proceed next?
Anyone else, feel free to help.
Simon Bridge
Science Advisor
Homework Helper
- 17,871
- 1,661
I'm wondering if it isn't just easier to multiply it out ... we just start with $$z^6-1=\left [ \frac{64j(1-j)}{1+2j} \right ]^6 = 64^6\left [ \frac{j+1}{2j+1} \right ]^6$$
After all:
##(j+1)^2=(j+1)(j+1)=-1+j+j+1=2j##
##(j+1)^4=(2j)(2j)=-4##
##(j+1)^6=-4(2j)=-8j##
... that doesn't look so bad.
Same for the denominator; then rationalize the denominator to get the RHS in form ##\alpha+j\beta## and procede polar of whatever from there ... ##z^6## is likely to be a pain in terms of ##a+jb## but it's doable in polar form - 2 equations, solve for a and b. Or solve for the amplitude and phase that give zeros and convert afterwards?
After all:
##(j+1)^2=(j+1)(j+1)=-1+j+j+1=2j##
##(j+1)^4=(2j)(2j)=-4##
##(j+1)^6=-4(2j)=-8j##
... that doesn't look so bad.
Same for the denominator; then rationalize the denominator to get the RHS in form ##\alpha+j\beta## and procede polar of whatever from there ... ##z^6## is likely to be a pain in terms of ##a+jb## but it's doable in polar form - 2 equations, solve for a and b. Or solve for the amplitude and phase that give zeros and convert afterwards?
timeforchg
- 18
- 0
Simon Bridge said:I'm wondering if it isn't just easier to multiply it out ... we just start with $$z^6-1=\left [ \frac{64j(1-j)}{1+2j} \right ]^6 = 64^6\left [ \frac{j+1}{2j+1} \right ]^6$$
After all:
##(j+1)^2=(j+1)(j+1)=-1+j+j+1=2j##
##(j+1)^4=(2j)(2j)=-4##
##(j+1)^6=-4(2j)=-8j##
... that doesn't look so bad.
Same for the denominator; then rationalize the denominator to get the RHS in form ##\alpha+j\beta## and procede polar of whatever from there ... ##z^6## is likely to be a pain in terms of ##a+jb## but it's doable in polar form - 2 equations, solve for a and b. Or solve for the amplitude and phase that give zeros and convert afterwards?
Hi Simon,
Is it possible to show me your method starting from $$z^6-1=\left [ \frac{64j(1-j)}{1+2j} \right ]^6$$ till the end equation $$z^6$$= ##a+jb##
please?
Simon Bridge
Science Advisor
Homework Helper
- 17,871
- 1,661
That last bit is notation.
If I just wanted to find the roots of ##z^6-1## I'd put ##z^6-1=0##, then expand z in terms of a and b as in ##(a+jb)^6-1=0##.
This is a bit like that, only you have another complex number, which is a constant, in there:
##z^6+1=C##
So I want to be able to write ##C=\alpha+j\beta## then I can just equate the real and imaginary parts for two simultaneous equations with two unknowns. That's the idea - the rest is strategy to make it look like that.
I was just wondering if the difficult-looking complex number is actually much simpler than it looks. We've been scared of multiplying out the power of six. After all, it should be easier to handle ##z^6-1=\alpha+j\beta## shouldn't it?
Anyway - to illustrate the point, I multiplied out the numerator for you ... it turns out to be quite simple. You'll have to do the rest I'm afraid.
Where does this come from - it seems unusually obnoxious for homework?
If I just wanted to find the roots of ##z^6-1## I'd put ##z^6-1=0##, then expand z in terms of a and b as in ##(a+jb)^6-1=0##.
This is a bit like that, only you have another complex number, which is a constant, in there:
##z^6+1=C##
So I want to be able to write ##C=\alpha+j\beta## then I can just equate the real and imaginary parts for two simultaneous equations with two unknowns. That's the idea - the rest is strategy to make it look like that.
I was just wondering if the difficult-looking complex number is actually much simpler than it looks. We've been scared of multiplying out the power of six. After all, it should be easier to handle ##z^6-1=\alpha+j\beta## shouldn't it?
Anyway - to illustrate the point, I multiplied out the numerator for you ... it turns out to be quite simple. You'll have to do the rest I'm afraid.
Where does this come from - it seems unusually obnoxious for homework?
timeforchg
- 18
- 0
Will try it out. Actually, this is not homework. I am just trying out past year exam questions. Sad to say, solutions is not provided. So I will never know whether I am doing it right or wrong.Simon Bridge said:That last bit is notation.
If I just wanted to find the roots of ##z^6-1## I'd put ##z^6-1=0##, then expand z in terms of a and b as in ##(a+jb)^6-1=0##.
This is a bit like that, only you have another complex number, which is a constant, in there:
##z^6+1=C##
So I want to be able to write ##C=\alpha+j\beta## then I can just equate the real and imaginary parts for two simultaneous equations with two unknowns. That's the idea - the rest is strategy to make it look like that.
I was just wondering if the difficult-looking complex number is actually much simpler than it looks. We've been scared of multiplying out the power of six. After all, it should be easier to handle ##z^6-1=\alpha+j\beta## shouldn't it?
Anyway - to illustrate the point, I multiplied out the numerator for you ... it turns out to be quite simple. You'll have to do the rest I'm afraid.
Where does this come from - it seems unusually obnoxious for homework?
Simon Bridge
Science Advisor
Homework Helper
- 17,871
- 1,661
Exam question? ... then, either look for a trick in the course-notes for the year, or that year covered similar examples in assignments so they'd remember some special approach.
timeforchg
- 18
- 0
SOLVED! Thanks a lot guys! Appreciate it.
Similar threads
- Replies
- 6
- Views
- 1K
- Replies
- 21
- Views
- 2K
- Replies
- 20
- Views
- 2K
- Replies
- 19
- Views
- 2K
- Replies
- 8
- Views
- 1K
- Replies
- 14
- Views
- 2K
- Replies
- 18
- Views
- 3K
- Replies
- 0
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 7
- Views
- 3K
Hot Threads
-
Geometry: Similar Shapes
- Started by paulb203
- Replies: 116
- Precalculus Mathematics Homework Help
-
[ASK] Trigonometric Inequality
- Started by Monoxdifly
- Replies: 6
- Precalculus Mathematics Homework Help
-
What does this equation mean?
- Started by inuka00123
- Replies: 12
- Precalculus Mathematics Homework Help
-
Finding polar equation of a shifted cricle
- Started by farfromdaijoubu
- Replies: 6
- Precalculus Mathematics Homework Help
-
Intersection of a circle and a sine curve
- Started by vcsharp2003
- Replies: 26
- Precalculus Mathematics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math