sylwesh98
- 42
- 0
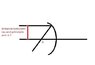
1. The problem statement: A ray of light is incident on a concave mirror. It is parallel to the principle axis and its height from principle axis is equal to the focal length of the mirror. the ratio of the distance of point B to the distance of the focus from the center of curvature is( AB is the reflected ray)
A)2/√3 B)√3/2 C)2/3 D)1/2
2. Answer to this problem give is: A
Have I done anything wrong?[/B]
A)2/√3 B)√3/2 C)2/3 D)1/2
2. Answer to this problem give is: A
The Attempt at a Solution
: the ray of light is parallel to principle axis so it should pass through the focus. the point of the focus and the point of intersection of the ray and the focus are same. so i thought the answer is 1.Have I done anything wrong?[/B]