SUMMARY
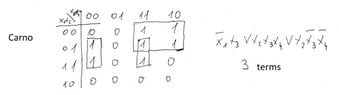
The discussion focuses on the minimization of the Perfect Disjunctive Normal Form (PDNF) using the Quine method and Karnaugh map for a function defined by the vector of values (2, 3, 4, 6, 7, 12, 15). The user, urugvai, encounters a discrepancy of one term between the results of the two methods. It is clarified that the second term from the Quine method can be omitted as it is already covered by the first and third terms, indicating that the Karnaugh map provides a more minimal representation.
PREREQUISITES
- Understanding of Perfect Disjunctive Normal Form (PDNF)
- Familiarity with the Quine minimization method
- Knowledge of Karnaugh maps for logic simplification
- Basic concepts of Boolean algebra
NEXT STEPS
- Study the Quine-McCluskey algorithm for minimization of Boolean functions
- Learn how to construct and interpret Karnaugh maps for four-variable functions
- Explore the differences between PDNF and other forms like Perfect Conjunctive Normal Form (PCNF)
- Investigate common pitfalls in logic minimization techniques
USEFUL FOR
Logic designers, computer scientists, and students studying digital logic design who are interested in optimizing Boolean functions through minimization techniques.