bbfcfm2000
- 10
- 0
I have a seemingly easy question I think...but wanted to run it by this board before I submitted my answer.
Homework Question
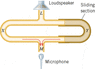
The sound produced by the loudspeaker in the (attached) drawing has a frequency of 10700 Hz and arrives at the microphone via two different paths. The sound travels through the left tube LXM, which has a fixed length. Simultaneously, the sound travels through the right tube LYM, the length of which can be changed by moving the sliding section. At M, the sound waves coming from the two paths interfere. As the length of the path LYM is changed, the sound loudness detected by the microphone changes. When the sliding section is pulled out by 0.0290 m, the loudness changes from a maximum to a minimum. Find the speed at which sound travels through the gas in the tube.
Is this a trick question? Isn't the speed of sound always 343 m/s?
Thank you in advance!
Homework Question
The sound produced by the loudspeaker in the (attached) drawing has a frequency of 10700 Hz and arrives at the microphone via two different paths. The sound travels through the left tube LXM, which has a fixed length. Simultaneously, the sound travels through the right tube LYM, the length of which can be changed by moving the sliding section. At M, the sound waves coming from the two paths interfere. As the length of the path LYM is changed, the sound loudness detected by the microphone changes. When the sliding section is pulled out by 0.0290 m, the loudness changes from a maximum to a minimum. Find the speed at which sound travels through the gas in the tube.
Is this a trick question? Isn't the speed of sound always 343 m/s?
Thank you in advance!