Dschumanji
- 153
- 1
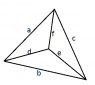
I was skimming through the book "The Divine Proportion a Study in Mathematical Beauty" by H.E. Huntley and found an interesting passage labeled "The Tetrahedron Problem." The problem is stated like this:
The faces of a tetrahedron are all scalene triangles similar to one another, but not all congruent, with integral sides. The longest side does not exceed 50. Show its network. The limitation to integral values being waived, show that the ratio of the length of the longest to that of the shortest edge has a limiting value, and find it.
This is how his solution begins:
Two triangles may have five parts of the one congruent with five parts of the other without being congruent triangles. If the triangles are not congruent, their congruent parts cannot include the three sides. Hence the triangles must be equiangular, and it is easily shown that the lengths of the sides must be in geometrical progression...
I've been scratching my head wondering what the hell this guy is trying to convey with the first two sentences (no images are provided in the text). What makes it even worse is the absence of a proof that the sides of whatever he is talking about MUST be in geomtric progression. Could anyone shed some light on this?
The faces of a tetrahedron are all scalene triangles similar to one another, but not all congruent, with integral sides. The longest side does not exceed 50. Show its network. The limitation to integral values being waived, show that the ratio of the length of the longest to that of the shortest edge has a limiting value, and find it.
This is how his solution begins:
Two triangles may have five parts of the one congruent with five parts of the other without being congruent triangles. If the triangles are not congruent, their congruent parts cannot include the three sides. Hence the triangles must be equiangular, and it is easily shown that the lengths of the sides must be in geometrical progression...
I've been scratching my head wondering what the hell this guy is trying to convey with the first two sentences (no images are provided in the text). What makes it even worse is the absence of a proof that the sides of whatever he is talking about MUST be in geomtric progression. Could anyone shed some light on this?
Last edited: