I The velocity of a moving frame of reference

[RossBlenkinsop]

TL;DR Summary

train carriages in a MFR

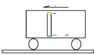
In the attached fig 1 you have a moving frame of reference (MFR) moving in the direction V at velocity V

Looking from above in the MFR there are 2 identical train carriages (car 1 and car 2), Car 1 is on a long set of tracks. Car 2 cannot move but is on train tracks.

There are also 2 Identical clocks, clock 1 and clock 2 which are attached to the train tracks. Clock 2 can receive electrical signals from car 2 thru the tracks . Clock 1 can receive electrical signals from car 1 thru the tracks

Car 1 can move along the train tracks in the direction v1 at a constant velocity v1

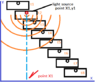
Fig 2 shows inside one of the train carriages, in it is a light tube of length L. The light tube has a light and detector at one and and a mirror at the other. The light tube has a wire that is connected to the train tracks . When photons are emitted by the light source in the light tube, an electric pulse is sent down the wire to the train tracks. The electric pulse flows along the train track back to the clock which starts the clock running .

When an electric pulse is sent it makes a mark on the train track, so the position of a train at the time the electric pulse was sent is known..

Back at the light tube, the photons are reflected by the mirror, in the light tube, back to the detector, in the light tube. When the photons arrive at the detector, in the light tube, a second electric pulse is sent down the wire, along the train tracks and back to the clock, which stops the clock, thus measuring the time it takes for light to traverse the length L. the length of the light tube

Both train carriages are identical in every way and both train carriages are set up in an identical fashion. They are identical in every way except one can move along the tracks, the other cant.

if the MFR is traveling in direction V at velocity V. When the velocity of Car 1 ( velocity V1) is equal to the velocity of the MFR (V) and when the direction of car 1 (direction of V1) is exactly opposite direction of the MFR (direction of V), the time to traverse the length of the light tube, in Car 1, will be the shortest.

Is that correct ?

From the above the velocity and direction of the MFR can be calculated

 

[jbriggs444]

There are a number of errors with the analysis of this experiment. One is that the "moving frame of reference" is never used. Another is that there is no accounting for signal delays in the wire in the train car or along the train tracks.

 

[RossBlenkinsop]

Im not sure using another terminology changes the overall result ?

the relevant time is the duration between pulse 1 and the second pulse. The delay will be the same for both pulses moving in the same direction along the same track, so the time difference between pulse 1 and pulse 2 will remain constant

 

[RossBlenkinsop]

the wires, train track, wheels etc etc are all at constant velocity, constant length, constant direction , constant ... constant constant

the delay for pulse 1 will be identical to the delay of pulse 2 , so the time difference between pulse 1 and pulse 2 will also be constant

any delay as a result of the train being slightly further away with pulse 2 can be accounted for by measuring the marks on the track and the speed of electricity thru the train track ...that was the purpose of the marks on the track as I anticipated that question

 

[RossBlenkinsop]

the speed of electricity thru the train track would be measured using a clock at rest wrt the train track

 

[Ibix]

Your description is over-complex, but you appear to have a light clock on a cart and to be measuring its tick rate in the track frame (once you correct for signal delay). This will just be one tick per $1/\sqrt{1-v_1^2/c^2}$ seconds, where $v_1$ is the velocity of the cart with respect to the track.

I fail to see how you think you can deduce anything about another frame of reference (your MFR). You do not appear to be making any measurements using it.

 

[RossBlenkinsop]

In order to clarify my logic

Referring to fig 99

There is a moving frame of reference ( MFR ) moving to the right at velocity MFRV

In the time between T1 and T2 the MFR moves a distance to the right of mfrD see to the left of fig 99

Inside the MFR there are three light clocks a green light clock (GLC), a red light clock (RLC) and a blue light clock (BLC)

The BLC is at rest wrt the MFR

The GLC is able to move to the left at a constant velocity GV

The RLC is able to move to the right at a constant velocity RV

RV = GV

In the time between T1 and T2 GV and RV move a distance of d see the small square top right

At time To the GLC and RLC are both at position X see the top of fig 99. There is a strobe light at position X . A To the strobe goes off

As it is difficult to represent diagrammatically I have drawn the MFR at time 0 at the top, T1 below that and T2 below that again.

At the bottom of fig 99 I have simply shown the position of the various clocks at To, T1 and T2, relative to X

At time T1 the GLC will be a distance of (mfrD – d) from X (the original position of the light source)

At time T1 the RLC will be a distance of (mfrD + d) from X (the original position of the light source)

At time T2 the GLC will be a distance of (mfrD + mfrD - d - d) from X (the original position of the light source)

At time T2 the RLC will be a distance of (mfrD + mfrD + d + d) from X (the original position of the light source)

The positions of the various clocks wrt the position X is shown at the bottom of fig 99

At the bottom of fig 99 I have shown the path taken by the photons in the RLC and GLC

At To the RLC and GLC will be at X
At T1 the GLC will be at GT1
At T1 the RLC will be at RT1
At T2 the GLC will be at GT2
At T2 the RLC will be at RT2

Any problems thus far ?

 

[jbriggs444]

In order to clarify my logic

Referring to fig 99

There is a moving frame of reference ( MFR ) moving to the right at velocity MFRV.

As I understand it, you have a set of tracks that are at rest relative to this frame. And you have a car (car 2) which is also at rest relative to this frame.

In the time between T1 and T2 the MFR moves a distance to the right of mfrD see to the left of fig 99

In what frame of reference are T1 and T2 measured? The above statement appears to pre-suppose that simultaneity is absolute.

 

[RossBlenkinsop]

appears there are no problems

as in the previous example the GLC and RLC are on train tracks and an electric pulse is transferred from the GLC and RLC to the train tracks for each tick of the RLC and GLC. The electric pulses flow back along the train tracks to the BLC which measures the duration between the pulses.

The BLC has a constant tick rate as it is tied to the MFR

will the tick rates of the GLC and RLC be the same or different ?

 

[RossBlenkinsop]

As I understand it, you have a set of tracks that are at rest relative to this frame. And you have a car (car 2) which is also at rest relative to this frame.

In what frame of reference are T1 and T2 measured? The above statement appears to pre-suppose that simultaneity is absolute.

T1 is the time that the light pulse strikes the bottom of the GLC and the RLC. The electric pulse then moves back along the train track to the BLC.

T1 is not actually measured I have just used To,T1 and T2 to demonstrate the chronology of events for the purposes of making my logic understandable .

The only thing that is "measured" is the duration between electric pulse 1 and electric pulse 2 off the train tracks by the BLC, ie how fast the RLC and GLC are ticking relative to the BLC

 

[RossBlenkinsop]

also in fig 99 I now have three cars sorry my fault that is confusing

there is a car at rest wrt MFR . That car houses the BLC

there is another car, not at rest wrt the MFR, it houses the GLC

there is another car, not at rest wrt the MFR, it houses the RLC

The RLC is moving at a constant velocity along train tracks to the right hand edge of fig 99

The GLC is moving at a constant velocity along train tracks to the left of fig 99

the velocity of the CLC is the same as the velocity of the RLC

I have omitted the cars tracks wheels etc etc as it make the picture too confusing I have just shown the moving clocks

 

[RossBlenkinsop]

sorry the other thing that is measured is the speed of electricity thru the train tracks, the marks on the tracks and the velocity and direction of the various train carriages moving wrt to the MFR

 

[RossBlenkinsop]

the purpose of the experiment is to adjust the velocity of the various trains, moving wrt the MFR, so that the clock tick rate, in the moving train carriage, is at its fastest as measured by the BLC

at a given velocity the tick rate should peak and then if the velocity is increased or decreased, from that specific value, the tick rate should slow

 

[PeterDonis]

the purpose of the experiment is to adjust the velocity of the various trains, moving wrt the MFR, so that the clock tick rate, in the moving train carriage, is at its fastest as measured by the BLC

The clock rate of a train, as measured by the BLC, will be fastest if it is at rest relative to the BLC. This is just a special case of the general result that, relative to any clock, a second clock will tick fastest if it is at rest relative to the first clock. There is no need for any complicated mathematical machinery to reach this result; it's a simple consequence of the relativistic time dilation formula.

 

[RossBlenkinsop]

in order to keep thing simple let's analyse only the 2D version

place the above models in a 2d Cartesian coord system

lets say when the strobe goes off it is at position x1,y1

assuming the entire experiment is moving, the entire experiment is moving away from that original position X1, Y1, at some rate V

appears to me if the train that can move is moving in the right direction and at the right rate so that it remains at position x1,y1

that will maximize the tick rate of that clock , in fact that will be the maximum tick rate for any clock in that frame

?

 

[jbriggs444]

in fact that will be the maximum tick rate for any clock in that frame

Which is what @PeterDonis just finished saying. It is a simple consequence of the time dilation formula.

That does not help you determine how fast the "moving frame of reference" is moving in any absolute sense.

 

[RossBlenkinsop]

I disagree that is what he said

I understand he said if the moving clock (GLC or RLC) is at rest wrt the BLC then that will be the maximum tick rate as measured by the BLC

I am saying if the RLC or GLC is at rest wrt to the origin of the light source, at point X1,Y1, then that will be the max tick rate

 

[RossBlenkinsop]

I refer to the attached image

u have a clock that is at rest wrt the source of the photons; clock 1
u have a second clock (clock 2) that is not at rest wrt the source of the photons

clock 2 simply must tick slower otherwise it defies physics

or am I missing something

 

[Ibix]

clock 2 simply must tick slower otherwise it defies physics

It must tick slower in the frame where the source is at rest. But in the frame where clock2 is at rest and the source and clock1 are in motion, clock1 will tick slower than clock2.

 

[PeterDonis]

I am saying if the RLC or GLC is at rest wrt to the origin of the light source, at point X1,Y1, then that will be the max tick rate

Max tick rate relative to which clock?

You were asking for the max tick rate relative to the BLC. That is what I answered.

If you want the max tick rate relative to some other clock, that will be a different answer. What state of motion gives the max tick rate depends on the state of motion of the clock you are measuring the tick rate relative to--the max tick rate relative to that clock will be for an object at rest relative to that clock. Which is the more general version of what I said.

 

[PeterDonis]

clock 2 simply must tick slower

Relative to clock 1, yes. "Tick rate" is relative.

or am I missing something

You appear to be missing that tick rate is relative.

 

[Ibix]

You appear to be missing that tick rate is relative.

...and/or that there's nothing special about the frame where the light emitter is at rest, at least as far as this experiment is concerned.

 

[Janus]

I refer to the attached image

u have a clock that is at rest wrt the source of the photons; clock 1
u have a second clock (clock 2) that is not at rest wrt the source of the photons

clock 2 simply must tick slower otherwise it defies physics

or am I missing something

What you seem to be missing is that the speed of light is invariant. It it is the same(c) relative to either frame as measured from that frame.

So, for example, if we start with both clocks at the same spot and the source (white dot) is at rest with respect to clock 1 (blue bar), then this is what happens according to the rest frame of clock 1.

The light expands outward at c from the source as clock 2(yellow bar) moves off to the right. The edge of the expanding light reaches the end of clock 1 before it reaches the end of clock 2.

However, in the rest frame of clock 2, this is what is happening:

The light expands outward from the point where it was emitted relative to clock 2, which at that moment coincides with the position of the light source and the top of clock 2. It expands outward at c from that point while both Clock 1 and the source move off to the left. You can't have the center of the expanding circle moving to the left along with the source, because then the left edge of the expanding light would have to be moving at more than c relative to clock 2 ( the right edge at less than c). Light must move at c in all frames.

The expanding light reaches the bottom of clock 2 before it reaches the bottom of clock 1.

 

[RossBlenkinsop]

I think ppl might be confusing what I refer to as a light source and being at rest wrt the light source.

see attached

there is a mfr with a light in the roof. At t2 the light briefly strobes at the point x1,y1. I am saying the moving clock in the MFR move in such a way that it remains at rest wrt the point X1,Y1

I have shown the photons at successive times t3 t4 t5 t6 as they spread out . There is a Cartesian coor system in dark blue and there is a light blue line to the point on the x-axis X1

as it is difficult to draw I have shown the position of the MFR at various time with t2 draw below t1 to show the rough chronology of events

I am saying if the moving train inside the MFR moves in such a way (in the right direction at the right rate) that it remains at rest wrt the point X1 Y1 then the clock within that train carriage must tick faster than any other clock in that frame. Those fast ticks will be transferred to the rail tracks and measured at the BLC. And the BLC will at all times be ticking slower than the clock at rest wrt the point X1Y1

 

[RossBlenkinsop]

or another way

The train carriage inside the MFR moves in the right direction and at the right rate so that it remains directly below (remains on a vertical line drawn thru the point X1) and at rest wrt the point X1Y1. I am saying if that is the case the tick rate of the clock in the moving train carriage will peak and that fast ticking will be transferred to the train tracks.

As the BLC is not at rest wrt the point X1 Y1 it must tick slower. Further as it is moving at some angle that is not perpendicular to a tangent of the photon wave fronts, it must tick slower.

 

[jbriggs444]

remains at rest wrt the point X1,Y1

Giving coordinates for a point without a coordinate system is pointless. If you want to say that there is a rest frame against which the moving frame moves, then say so. Of course it is equally valid to say that the moving frame is at rest and the rest frame moves.

 

[RossBlenkinsop]

coord added

the light blue line is a vertical line drawn to the point X1

if the train carriage remains on that line and at rest wrt to that line then its light clock will tick at the max

In order for that to happen the train carriage must be moving at the same rate as the MFR but in the opposite direction

If my logic is right every other non accelerating clock in that frame will tick slower

also if my logic is right if the train carriage is moving at the right rate and in the right direction, but is not on the blue line , then its clock will stop working

 

[jbriggs444]

also if my logic is right if the train carriage is moving at the right rate and in the right direction, but is not on the blue line , then its clock will stop working

Clocks are real. Coordinates are just scribbles written down on a piece of paper. Scribbles written on a piece of paper cannot prevent a clock from working. It follows that your logic is wrong.

 

[Ibix]

I think ppl might be confusing what I refer to as a light source and being at rest wrt the light source.

Which of the clocks is at rest with respect to the light source is irrelevant. The speed of light is independent of its source. Your diagrams - if you draw them accurately - will be the same however the light source is moving.

there is a mfr with a light in the roof

I think you do not know what a "frame of reference" is. What you are describing here is a box with a light on the roof. A frame of reference is a choice of how you define "at rest". It is an abstract concept and does not and cannot have a roof.

There are potentially two sensible reference frames here - the one you are using in which the box you've labelled "MFR" is moving but one of the light clocks isn't, and another frame in which the box you've labelled "MFR" isn't moving. You have used the former frame for everything and never the latter. Thus you always find the clock at rest as described by this frame ticks fastest. Simply putting it in a box changes nothing about it.

However, if you re-analyse your experiment in a frame of reference where the box you've labelled MFR is at rest you will find that the tick rates of the clocks are switched because the clock that's stationary in your diagram is moving in the new diagram. This is what @Janus drew in his second diagram a few posts back.

 

[Nugatory]

I think ppl might be confusing...

That’s likely, but some of the confusion may be due to your very non-standard terminology.

For example, you say things like “there is a mfr with a light in the roof”, and it is far from clear what that means. To see the difficulty, consider that a frame of reference is basically a mathematical convention for assigning coordinates to points in spacetime (formally called “events”) so you’re saying “there is a moving mathematical convention with a light on the roof”... and that is not something easily understood.

Any time you say something about a frame of reference, you should be able to reword what you’re saying to use the phrase “using the coordinates assigned by” the frame. People don’t always do this because it leads to clumsy and verbose English sentences and no one naturally speaks that way, but if they can’t do it what they’re saying will make no sense.

 

[RossBlenkinsop]

actually I think the frame chosen is irrelevant the simple question is if one of the moving light clocks is at rest wrt the point X1 Y1 will the time difference between the electric pulse delivered to the train tracks peak as measured by any other identical clock, not a rest wrt that point

and

as the direction of one of the moving light clocks, and the rate of movement of one of the moving light clocks, in any frame of reference, approaches a state where it is approaching being at rest wrt the point X1 Y1 will the time difference between the electric pulse approach a peak as measured by any other identical clock, not a rest wrt that point

appears to me the frame is irrelevant

any identical clock, in any frame, not at rest wrt the point x1 y1 will tick slower than an identical clock at rest wrt the point x1 y1

 

[RossBlenkinsop]

if an experiment can be devised where a light clock remains at rest wrt the point x1 y1 then that will be the peak tick rate for that clock in any frame and any other identical clock in any other frame will tick slower than that clock

I believe above I have devised such an experiment

 

[Ibix]

the point X1 Y1

This point is only a point in one frame. Basing an argument on the use of "a point" implies a frame.

It is true that your electrical signals are invariant, but this simply reflects the speed of the clock with respect to the rails. The same could be achieved with a radar set.

 

[RossBlenkinsop]

of course the light clock needs to be oriented is such a way that the long axis of the light clock is parallel to the incoming photons from the point X1 Y1

 

[Ibix]

I believe above I have devised such an experiment

Seriously? You think no one in over a century has ever considered two light clocks in relative motion? You're still well inside territory competent undergrads explore routinely. You're just analysing it incorrectly.

 

[RossBlenkinsop]

"the point is only a point in one frame"

a strobe goes off and photons emanate from that point in straight lines in all directions

the speed of photons is invariant in all frames

if in 1 million yrs time I meticulously traced those photons back along their trajectories to the point from which they emanated. is that an arbitrary point ?

 

[RossBlenkinsop]

for me to be wrong would be a breach of the laws of physics

 

[Ibix]

is that an arbitrary point ?

Yes. It depends which frame you use what that point is. Janus' two diagrams demonstrate this clearly. But it should be obvious.

Work in a frame where the light source is at rest. It emits a spherical wavefront. Backtrace the rays and you get to the light source.

Now work in a frame where the lightsource is moving. It emits a spherical wavefront. Backtrace the rays and you get to the place where the light source was, not where it is now. Thus this is a different point from the previous paragraph.

 

[RossBlenkinsop]

because the speed of light is invariant regardless of the elapsed time period elapsed tracing the trajectories of those photons will always lead back to the same point

its almost as if the point is at an absolute position in space

 

[RossBlenkinsop]

Yes. It depends which frame you use what that point is. Janus' two diagrams demonstrate this clearly. But it should be obvious.

Work in a frame where the light source is at rest. It emits a spherical wavefront. Backtrace the rays and you get to the light source.

Now work in a frame where the lightsource is moving. It emits a spherical wavefront. Backtrace the rays and you get to the place where the light source was, not where it is now. Thus this is a different point from the previous paragraph.

In both instances u retrace the photons trajectory to the point from which they emanated ! Just so happens in scenario 1 the actual light itself is at rest wrt the point x1 y1 ...your basically agreeing with me

 

[Ibix]

because the speed of light is invariant regardless of the elapsed time period elapsed tracing the trajectories of those photons will always lead back to the same point

You're clearly not even reading what I write, now. I just explained how this is not the case. Please re-read post #38 and say what you do not understand.

its almost as if the point is at an absolute position in space

This has been known to be meaningless for around three and a half centuries.

 

[RossBlenkinsop]

its almost as if the point is at an absolute position in space

that point cannot move, if it did that would mean the speed of light is not invariant

 

[Ibix]

In both instances u retrace the photons trajectory to the point from which they emanated ! Just so happens in scenario 1 the actual light itself is at rest wrt the point x1 y1 ...your basically agreeing with me

I am not even slightly agreeing with you. You claim that the place where the light is and a place where it isn't are the same place. That is clearly nonsense.

 

[RossBlenkinsop]

because the speed of light is invariant the 2 or more photons on the wave front must be exactly the same distance from the point X1 Y1 for all time

or in other words tracing back along the trajectories will always lead back to the same point, regardless of the frame used or the time period elapsed

 

[RossBlenkinsop]

or in other words the location of that point remains the same over time
and I am pretty sure if the location of something remains the same over time then that is the definition of "not moving"

 

[Ibix]

point X1 Y1

Again, this point is only stationary in one frame. In other frames, this point is moving and does not remain at the centre of the pulse.

in other words tracing back along the trajectories will always lead back to the same point

...but different frames will not agree what this point is and will all regard all other frames' "same points" as changing position.

in other words the location of that point remains the same over time

...according to the frame used to do the backtracing. Every other frame will come up with a stationary point too. But the whole point of different frames of reference is that they don't agree with each other what "stationary" means. They all regard the others' "stationary points" as moving, so there is no "absolutely stationary".

Look. Say the pulse is emitted at the origin in some frame. After time $t$ the pulse is at $x,y$ coordinates that satisfy $c^2t^2=x^2+y^2$. Always centred on $x,y=0,0$.

In another frame, the pulse was also emitted at the origin. After time $t'$ the pulse is at $x',y'$ coordinates that satisfy $c^2t'^2=x'^2+y'^2$. Always centred on $x',y'=0,0$.

But what is the Lorentz transform of $x,y=0,0$? It's $x',y'=-\gamma vt,0$, which is a moving point. The frames do not agree on what "where the light was emitted" means, except at the instant it was emitted.

I don't think I can state it more clearly than that, and it's 1am here. Signing off.

 

[Ibix]

Ugh. Thought of a way that might be clearer to you.

You agree that the strobe light is moving in one frame and stationary in the other. Thus it is (to use your terminology) "at rest with respect to X1,Y1" in one frame and not the other. But one of your light clocks was stationary with respect to the strobe light while the other was stationary in the frame where the strobe light is moving. Thus, which clock is "at rest with respect to X1,Y1" is different in the two frames.

Therefore the two frames disagree which clock ticks fastest.

I've put scare quotes around "at rest with respect to X1,Y1" because it's horrible and potentially misleading notation. It can, however, be made rigorous by adding bouys at the relevant coordinates at rest in the relevant frames. Naturally, they are moving with respect to one another.

Now I'm really going to sleep.

 

[Nugatory]

because the speed of light is invariant regardless of the elapsed time period elapsed tracing the trajectories of those photons will always lead back to the same point

That's just plain wrong, unless you are using the word "point" to mean a point in spacetime as opposed to a point in space (in which case we have more confusion from you using words differently than everyone else and should be using the word "event" because that's something completely different than a point in space).

or in other words the location of that point remains the same over time
and I am pretty sure if the location of something remains the same over time then that is the definition of "not moving"

No, the phrase "not moving" is completely meaningless unless you say what the the object in question is at rest relative to. And even then there's a lot to be said for being precise: "Using the coordinates assigned by a frame in which the spatial coordinates do not change...". This is some of what @Ibix was getting at in the post above when he said

I've put scare quotes around "at rest with respect to X1,Y1" because it's horrible and potentially misleading notation. It can, however, be made rigorous by adding bouys at the relevant coordinates at rest in the relevant frames. Naturally, they are moving with respect to one another.

If you can get hold of a copy of Taylor and Wheeler's book "Spacetime Physics", you will find it very helpful. An internet forum like this one is pretty good at pointing out errors and helping people over isolated hard spots, but not the best way of unwinding misunderstandings.

 

[Janus]

because the speed of light is invariant the 2 or more photons on the wave front must be exactly the same distance from the point X1 Y1 for all time

or in other words tracing back along the trajectories will always lead back to the same point, regardless of the frame used or the time period elapsed

You have three objects, A, B, and C in relative motion with respect to each other and all passing each other the same moment. As they pass each other, a light flash is emitted from them.
According to B, events unfold like this:

However, according to C, events unfold like this:

and according to A, they unfold like this:

Each of them measures the light flash as expanding out away from themselves at c.

If, after the last frame of each of these animations, you were to ask each of them to "retrace the light pulse to its origin, they would trace it back to themselves. But A B and C have separated and in three different points in the last frame, and so they would not agree that the rays trace back to the same spot.

 

[RossBlenkinsop]

well there is an absolute fact

if the speed of light is indeed invariant, regardless of what anyone perceives in any frame, measures in any frame doesn't measure in any frame what ever

if a light strobes at a point X1 Y1 simple maths tells us that 3 photons in the wave front will always triangulate back to the same point in space, for all time or aka that point remains in the same location for all time

if they don't triangulate back to that point then that means the speed of light is not invariant

so which is it is the speed of light not invariant or do the photons triangulate to a set point in space ?