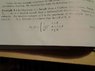Therefore, since P(A) = 0, we have convergence in probability.

[Artusartos]

I was a bit confused with the pages that I attached...

1) "An intuitive estimate of \theta is the maximum of the sample". But we are only taking random samples, so even the maximum might be far from \theta, right?

2) I don't understand how E(Y_n) = (n/(n+1))\theta. I thought that E(Y_n) = (Y_n)*pdf = (Y_n)(\frac{nt^n-1}{\theta^n}).

3) "Further, based on the cdf of Y_n, it is easily seen that Y_n \rightarrow \theta". Does that mean that E(Y_n) converges to theta, so Y_n must also converge to theta?Thank you in advance

 

[Stephen Tashi]

Some of those questions are explained in this thread:

https://www.physicsforums.com/showthread.php?t=380389

 

[Artusartos]

Some of those questions are explained in this thread:

https://www.physicsforums.com/showthread.php?t=380389

Thank you for the link. It was very helpful...but I'm still a bit confused about my first and last questions...

 

[Stephen Tashi]

1) "An intuitive estimate of \theta is the maximum of the sample". But we are only taking random samples, so even the maximum might be far from \theta, right?

Correct. The story of life in probability theory is that there is no deterministic connection between probability and actuality. The important theorems that mention random variables and actual oucomes only speak of the probability of certan actualities (which has a circular ring to to it). The best you can do is find an actuality that has a probability of 1 as some sort of limit is approached.

 

[mathman]

Thank you for the link. It was very helpful...but I'm still a bit confused about my first and last questions...

For your first question - you are right. The maximum is a good guess, but it could easily be wrong.

For you third question, define Y_n.

 

[Artusartos]

For your first question - you are right. The maximum is a good guess, but it could easily be wrong.

For you third question, define Y_n.

Y_n is the maximum of X_1, ... , X_n. Do we need to look at what E(Y_n) approaches in order to see what Y_n approaches to?

 

[mathman]

Since E(Y_n) -> θ and θ is the maximum of the distribution, the probability that lim Y_n is < θ must be 0.

The proof is straightforward. Let A be the event that the limit is < θ, then:

E(Y_n) = E(Y_n|A)P(A) + E(Y_n|A')P(A') -> θ only if P(A) = 0.