Thin film (interference problem)

[Sefrez]

Homework Statement

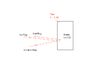
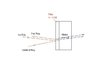
A sheet of glass having an index of refraction of 1.20 is to be coated with a film of material having an index of refraction of 1.42 such that green light with a wavelength of 525 nm (in air) is preferentially transmitted via constructive interference.

What is the minimum thickness of the film that will achieve the result?

Homework Equations

See my solution.

The Attempt at a Solution

I did this problem and end up with a thickness half that of the answer. Here is what I did.

I first noted that on the first reflection, there is a phase shift of ∏. This is because it there is reflection on a surface of higher index. For the second reflection, there is no phase shift as the glass index is lesser than the film. So the total phase shift due to reflection is just ∏.

Then the total phase shift should be related with: Δ∅ = ∏ + 4∏nL/λ, where n = index of refraction of film, L = thickness of film, λ = wavelength of light in vacuum. In order for there to be constructive interference, this phase shift must be equal to 2∏m where m is an integer.

So:
∏ + 4∏nL/λ = 2∏m
1/2 + 2nL/λ = m
2nL/λ = m - 1/2
L = λ(m - 1/2) / (2n), m >= 1

In order to minimize L, I set m = 1. So:

L = λ(1/2) / (2n) = 1/4 λ/n = 1/4 525 nm / 1.42 = 92.23 nm

The answer state is 184.46 nm.

Am I incorrect or is it?
Thanks!

 

[ehild]

Make a drawing. Where is the first reflection for the transmitted light?

ehild

 

[Sefrez]

I am unsure if you meant for myself or a drawing here. I made one here so that you can see how I am interpreting the problem. Ray 1 has a phase shift of λ/2 from reflection, but Ray 2 does not.

 

[ehild]

I am unsure if you meant for myself or a drawing here. I made one here so that you can see how I am interpreting the problem. Ray 1 has a phase shift of λ/2 from reflection, but Ray 2 does not.

That is the reflected beam, and you need to have maximum transmittance. That occurs if there is destructive interference in the reflected beam.

ehild

 

[Sefrez]

Oh, I interpreted that it wanted minimum transmittance:

is preferentially transmitted via constructive interference.

I guess that is not what it says.

 

[ehild]

"Preferentially transmitted" means maximum transmittance. So constructive interference happens in the transmitted beam (blue rays in the figure).

ehild

 

[Sefrez]

Yeah, I wasn't sure what it meant by "preferentially" and "constructive interference." After seeing the figure with the added rays, I now see constructive interference is not referring to the rays to the left!

Also, thanks for drawing that. I was going to ask what correlated maximum transmission with minimum reflection considering that interference is an after the fact (it happens after the ray exits the film.) But now I see that the difference between the two phase differences (left rays and right rays) is always 180 degrees. Is that correct?

 

[ehild]

One transmitted ray goes directly through the layer, the other one first reflects from the layer-glass interface (no phase change) goes backwards through the layer again, reflects from the layer-air interface (no phase change) and goes through the layer once more. The phase difference is solely because of the path difference, so 4∏nL/λ = 2∏m to get maximum transmittance.
If there is no absorption, the transmitted plus reflected intensity = incident intensity. If the reflectance is minimum at a certain wavelength, the transmittance is maximum and vice versa. ehild

 

[Sefrez]

Yeah, I think I should re-phrase what I said, "is always 180 degrees" to "is 180 degrees when the other is a maximum or a minimum." I imagine if the rays on the left were at a phase difference of ∏/2, then the same would be true for the rays at the right - that is, both intermediate reflection and transmission. Thanks. :)