Third Invariant expressed with Cayley-Hamilton Theorem

[FluidStu]

The Cayley-Hamilton Theorem can be used to express the third invariant of the characteristic polynomial obtained from the non-trivial solution of the Eigenvector/Eigenvalue problem. I follow the proof (in Chaves – Notes on Continuum Mechanics) down to the following equation, then get stuck at "Replacing the values of I_T and II_T with those in 1.269. Could someone please explain? Thanks

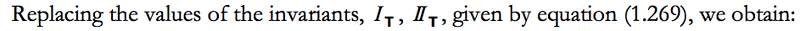
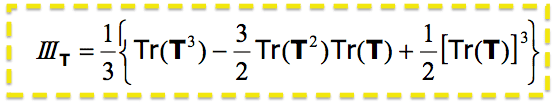
with 1.269 being:

 

[andrewkirk]

We need to show that the RHS of the equations in the first two boxes are equal. To minimise the latex coding I'll write $A$ for $Tr(T)$ and $B$ for $Tr(T^2)$. Then subtract the RHS of the second from the RHS of the first and multiply the result by 2 to get:
$$2II_TA-2I_TB-A^3+3AB=2II_TA-2AB-A^3+3AB=A\left(2II_T-2B-A^2+3B\right)=A\left(2II_T+B-A^2\right)=2A\left(II_T-0.5(A^2-B)\right)
=2A\left(II_T-II_T\right)=0$$
So twice the difference is zero.
So the two RHSs are equal.

 

[FluidStu]

Great! Thanks Andrew.