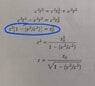Woopa
- 20
- 4
- Homework Statement
- Time dilation derivation
- Relevant Equations
- Pythagoras theorem
Hi this is my first post the forum, nice to meet you all.
I am trying to derive the time dilation formula following the image attached. However I am unsure of the algebra being used toget from the 2nd line of working to the 3rd line. Can someone please tell me what the name of the algebra concept being used is and some resources I can use to understand it.
Thank you!
I am trying to derive the time dilation formula following the image attached. However I am unsure of the algebra being used toget from the 2nd line of working to the 3rd line. Can someone please tell me what the name of the algebra concept being used is and some resources I can use to understand it.
Thank you!