AishaGirl
- 10
- 0
Hello, AQA is a British exam board and on their paper they have a list of equations. Can someone tell me why the time dilation equation is to the power -1/2?
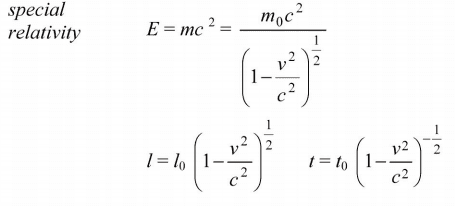
Thanks.
Thanks.