Time for falling down the incline (Rotating Solid Cylinder)

[andyrk]

Homework Statement

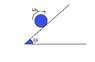
A solid cylinder of radius R is spun and then placed on an incline having coefficient of friction μ=tanθ
(θ is the angle of the incline). The solid cylinder continues to spin without falling for time:
(A)Rω_o/3gsinθ
(B)Rω_o/2gsinθ
(C)Rω_o/gsinθ
(D)2Rω_o/gsinθ

The Attempt at a Solution

The solution that I could think of was firstly related to what the question said. It says time elapsed until it starts falling down. So I assumed that that means the time for which the cylinder will keep rotating on the place on the incline it was placed when it was first spun.

So, the equations came out to be:
Let 'm' be the mass of the cylinder. Then,
mgsinθ+mRα=μmgcosθ
=>gsinθ+Rα=mgcosθ (condition for cylinder to be where it was initially)

But using this equation, there is no way I can find out the time taken for the cylinder to start coming down. And I don't see any other way to do so either. So need help on this matter. Reply ASAP. Thanks :)

 

[andyrk]

Anyone there?? Please reply people!

 

[dauto]

Where did you get the equation
mgsinθ+mRα=μmgcosθ ?
It is not right. What you need to do is to find the applied torque (due to friction force) and calculate how long it will take for that torque to drain all the initial angular momentum and stop spinning at which point it starts rolling down the ramp

 

[haruspex]

What you need to do is to find the applied torque (due to friction force) and calculate how long it will take for that torque to drain all the initial angular momentum and stop spinning at which point it starts rolling down the ramp

It can also be done through angular acceleration, but I agree there are several things wrong with the OP equations:

mgsinθ+mRα=μmgcosθ

What you need is a torque equation.
It is a solid cylinder. What is the moment of inertia of a solid cylinder? What torque is required to produce an angular acceleration of α?
What point are you taking torques about? What is the torque of each of your two forces about that point?

=>gsinθ+Rα=mgcosθ

Is that just a typo, or did you cancel incorrectly?

 

[andyrk]

Thanks! I agree the equation i put forward is wrong. But the following equation is correct, right?:

mgsinθ=μmgcosθ

My question is why is this equation true? This means that the cylinder NEVER moves away from the position it was placed in when it was spun. Which is clearly not true, since the question itself says "Time until it starts coming down the incline".

 

[Vibhor]

Thanks! I agree the equation i put forward is wrong. But the following equation is correct, right?:

mgsinθ=μmgcosθ

My question is why is this equation true?

What is the force equation for the cylinder i.e what do you get when you do ∑F =ma ?

 

[andyrk]

What is the force equation for the cylinder i.e what do you get when you do ∑F =ma ?

Yup.It would be:mgsinθ-μmgcosθ=ma

And a would be equal to 0. But why would that be? That means that the cylinder NEVER moves. Which is clearly not correct.

 

[Vibhor]

Yup.It would be:mgsinθ-μmgcosθ=ma

And a would be equal to 0. But why would that be? That means that the cylinder NEVER moves. Which is clearly not correct.

If ∑F =0 ,don't you think a = 0 ;) i.e if the net force on the object is zero then the object doesn't accelerate .

And yes, the object doesn't move and keeps spinning on its place .When spinning ceases ,it moves down.

 

[andyrk]

If ∑F =0 ,don't you think a = 0 ;) i.e if the net force on the object is zero then the object doesn't accelerate .

And yes, the object doesn't move and keeps spinning on its place .

Eh? But the question says: "Find the time till the cylinder keeps spinning and then starts MOVING DOWN". So that means, there is a net force down the incline..which was not so in the beginning and so there a net acceleration down the incline too, which was not their in the beginning. Got confused because of that. I think the question says that the cylinder first spins and after a certain time (which is to be calculated) friction cancels all the initial Angular Velocity (ω), the cylinder starts coming down. But you say it doesn't move and keeps spinning on its place. That would make time t=∞ (time taken for the cylinder to start coming down) as the cylinder would never come down. So I am still confused.

 

[Vibhor]

Eh? But the question says: "Find the time till the cylinder keeps spinning and then starts MOVING DOWN". So that means, there is a net force down the incline..which was not so in the beginning and so there a net acceleration down the incline too, which was not their in the beginning.

The net force mgsinθ - μN would be zero till the cylinder is spinning .After spinning stops ,there would be a net downward force which would cause the cylinder to move down .

Got confused because of that. I think the question says that the cylinder first spins and after a certain time (which is to be calculated) friction cancels all the initial Angular Velocity (ω), the cylinder starts coming down. But you say it doesn't move and keeps spinning on its place.

The cylinder would spin ,but the angular velocity is gradually reduced due to angular acceleration by the frictional torque .When the spinning ceases ,the cylinder moves down .

You need to find the time till the cylinder spins in its place .

 

[andyrk]

The net force mgsinθ - μN would be zero till the cylinder is spinning .After spinning stops ,there would be a net downward force which would cause the cylinder to move down .

What would be the cause of this downward force which was not present earlier, so as to make the cylinder move down this time?

 

[Vibhor]

The downward force acting on the cylinder is always mgsinθ .First friction opposes this downward force causing the cylinder to spin in its place .When it stops spinning ,friction is zero for a moment .Just as the cylinder starts to move downwards under the influence of mgsinθ ,friction again comes into scene opposing the motion .But now the cylinder starts to rotate in opposite direction to what it was initially .

 

[andyrk]

The downward force acting on the cylinder is always mgsinθ .First friction opposes this downward force causing the cylinder to spin in its place .When it stops spinning ,friction is zero for a moment .Just as the cylinder starts to move downwards under the influence of mgsinθ ,friction again comes into scene opposing the motion .But now the cylinder starts to rotate in opposite direction to what it was initially .

So friction firstly comes into play initially, then disappears when the cylinder has stopped spinning and then appears again when the cylinder has started coming down? It is absent just for that split second when the cylinder stops spinning, and mgsinθ is responsible for bringing it down in that split second? Does the cylinder eventually stop after that split second, or does it keep coming down? From your reasoning, I am able to conclude that cylinder eventually stays at the place it is.

 

[Vibhor]

So friction firstly comes into play initially, then disappears when the cylinder has stopped spinning and then appears again when the cylinder has started coming down? It is absent just for that split second when the cylinder stops spinning, and mgsinθ is responsible for bringing it down in that split second?

Yes .

Does the cylinder eventually stop after that split second, or does it keep coming down? From your reasoning, I am able to conclude that cylinder eventually stays at the place it is.

No .

It moves down ,but with a constant speed .The acceleration will again be zero .But zero acceleration means that the speed is constant. Initially it slips but gradually the cylinder spins faster and there will be a time (if the inclined plane is long enough ) that the cylinder rolls without slipping :)

 

[ehild]

Friction opposes the relative motion of the surfaces in contact. When spinning, the surface in contact with the incline moves downward, so the sliding friction acts upward, opposing the component of gravity. At the same time, this force of friction provides a counter-clockwise torque about the axis of the cylinder which makes the spinning slow down. When the spinning stops, the surfaces in contact do not move, and the friction gets static. That static friction keeps the contact points, a line, fixed to the incline and that unmoving line serves as instantaneous axis of rotation. The component of gravity along the incline acts at the CM of the cylinder and it will turn the cylinder anti-clockwise around the instantaneous axis, so it gets rolling down.
When rolling, the speed of the centre of mass is related to the angular speed ω: V=ωR. The cylinder moves along the incline with acceleration determined by the forces acting on it: the component of gravity, mgsin(θ) and the upward static friction Fs. Fs≤μmgcos(θ):
ma =mgsin(θ)-Fs.
The torque of the static friction accelerates the rotation about the CM with angular acceleration α:
Iα=RFs
When rolling, V=Rω and dV/dt=Rdω/dt, so you can substitute α=a/R. eliminating Fs, you find the acceleration of the cylinder down the incline.


ehild

 

[andyrk]

It moves down ,but with a constant speed .The acceleration will again be zero .But zero acceleration means that the speed is constant. Initially it slips but gradually the cylinder spins faster and there will be a time (if the inclined plane is long enough ) that the cylinder rolls without slipping :)

Why would cylinder gradually begin to spin faster? As friction ( and as a result frictional torque) remains same and radius R also remains same and velocity of CM also remains same, so ω also stays same? As v=Rω? Right? So why would the cylinder start to spin faster?

 

[andyrk]

Friction opposes the relative motion of the surfaces in contact. When spinning, the surface in contact with the incline moves downward, so the sliding friction acts upward, opposing the component of gravity. At the same time, this force of friction provides a counter-clockwise torque about the axis of the cylinder which makes the spinning slow down. When the spinning stops, the surfaces in contact do not move, and the friction gets static. That static friction keeps the contact points, a line, fixed to the incline and that unmoving line serves as instantaneous axis of rotation. The component of gravity along the incline acts at the CM of the cylinder and it will turn the cylinder anti-clockwise around the instantaneous axis, so it gets rolling down.


ehild

Thanks a lot ehild! This was really great help and explanation. :) :D

 

[Vibhor]

Why would cylinder gradually begin to spin faster?

When the cylinder stops spinning ω = 0 .The frictional torque then provides the angular acceleration ,which causes the cylinder to spin faster .

As friction ( and as a result frictional torque) remains same and radius R also remains same and velocity of CM also remains same, so ω also stays same? As v=Rω? Right? So why would the cylinder start to spin faster?

No . v=Rω holds when the cylinder rolls without slipping .But that is not the case initially when the cylinder starts to move down the inclined plane . v>Rω for some time . ω gradually increases ,and there will come a time (assuming inclined plane is long) that v = Rω . Now the cylinder happily rolls without slipping down the inclined plane .

 

[andyrk]

When the cylinder stops spinning ω = 0 .The frictional torque then provides the angular acceleration ,which causes the cylinder to spin faster .



No . v=Rω holds when the cylinder rolls without slipping .But that is not the case initially when the cylinder starts to move down the inclined plane . v>Rω for some time . ω gradually increases ,and there will come a time (assuming inclined plane is long) that v = Rω . Now the cylinder happily rolls without slipping down the inclined plane .

Haha.. Happy Endings
Thanks, got that one now.

 

[ehild]

At the moment when the rolling stops and the cylinder is still static the condition of rolling V=Rω holds.
The component of gravity turns the CM around the instantaneous axis, (shown by the red dot in the figure) so the cylinder starts to rotate and its CM also moves forward.
The static friction is less than the sliding friction, so there is a net downward force acting on the cylinder: it will accelerate downward, also its angular speed will increase so the rolling condition is maintained. I edited my previous post meanwhile, see the derivation there. The cylinder will accelerate downward, but a<gsin(θ)

ehild

 

[Vibhor]

At the moment when the rolling stops and the cylinder is still static the condition of rolling V=Rω holds. The static friction is less than the sliding friction, so there is a net downward force acting on the cylinder: it will accelerate downward, also its angular speed will increase so the rolling condition is maintained. I edited my previous post meanwhile, see the derivation there. The cylinder will accelerate downward, but a<gsin(θ)

ehild

I think in this problem ,we are always dealing with kinetic friction and not static friction .

When the cylinder stops spinning ,friction vanishes for a moment .The cylinder starts to slip down and as soon as it slips ,kinetic friction comes into scene . The acceleration would be mgsinθ - μN i.e 0 . But in the mean time the cylinder has picked up some speed downwards .The cylinder then moves down with constant speed . It slips for some time and afterwards it rolls without slipping.

 

[ehild]

v=Rω holds when the cylinder rolls without slipping .But that is not the case initially when the cylinder starts to move down the inclined plane . v>Rω for some time . ω gradually increases ,and there will come a time (assuming inclined plane is long) that v = Rω . Now the cylinder happily rolls without slipping down the inclined plane .

Initially bot V= and ω=0, so the spinning condition holds from the beginning. The static friction is just enough to keep the points of contact of the cylinder with the incline unmoved. Remember that mgsinθ-μmgcosθ=0. The cylinder does not start to slip. The points of contact serve as instantaneous axis of rotation, and the torque of gravity causes the CM rotating about the instantaneous axis which means both linear and angular acceleration at the same time.

ehild

 

[ehild]

I think in this problem ,we are always dealing with kinetic friction and not static friction .

The friction is kinetic while the cylinder is spinning at the same place. When the surfaces in contact do not move the friction is static. Kinetic friction occurs between surfaces moving with respect to each other.

When the cylinder stops spinning ,friction vanishes for a moment .The cylinder starts to slip down and as soon as it slips ,kinetic friction comes into scene . The acceleration would be mgsinθ - μN i.e 0 . But in the mean time the cylinder has picked up some speed downwards .The cylinder then moves down with constant speed . It slips for some time and afterwards it rolls without slipping.

Why should the friction vanish? The surfaces are still in contact, there are adhesion forces between them. The cylinder can not slip down as μ=tanθ, which just hinders slipping. The kinetic friction becomes static. The cylinder starts to rotate about the instantaneous axis, but that means also the forward motion of the CM.

ehild

 

[Vibhor]

Fine . May be you are right .Help me understand your view point .

1) Are you suggesting that after the cylinder stops spinning ,it immediately rolls down without slipping i.e it never slips in its entire journey downwards ?

2) What is the cause of the initial speed of the cylinder downwards after it stops spinning ? The net force on the cylinder is always mgsinθ - μN i.e 0 ?

3) Are you suggesting that the magnitude of static friction is f < μN when the cylinder is static and gradually increases its value to μN . This means there is a variable downward force mgsinθ - f for some time and as the static friction reaches its peal value μN then the net downward force becomes 0 after some time ?The cylinder then moves with constant speed .

Is this what you are suggesting ?

Pardon me if I have misunderstood you . I am trying to learn something good from you :)

 

[ehild]

Fine . May be you are right .Help me understand your view point .

1) Are you suggesting that after the cylinder stops spinning ,it immediately rolls down without slipping i.e it never slips in its entire journey downwards ?

Yes

2) What is the cause of the initial speed of the cylinder downwards after it stops spinning ? The net force on the cylinder is always mgsinθ - μN i.e 0 ?

There is no initial speed downward. Initially, the cylinder is in rest, neither translating, nor rotating. V=0, ω=0.

3) Are you suggesting that the magnitude of static friction is f < μN when the cylinder is static and gradually increases its value to μN . This means there is a variable downward force mgsinθ - f for some time and as the static friction reaches its peal value μN then the net downward force becomes 0 after some time ?The cylinder then moves with constant speed .

Is this what you are suggesting ?

Pardon me if I have misunderstood you .

No.
The magnitude of static friction never exceeds μs times the normal force N: Fs≤μsN, and μs is usually greater than the coefficient of kinetic friction. In this problem, the kinetic friction is enough to prevent downward acceleration. As the initial speed is zero, the cylinder will not slide down. At the last moment of the spinning, the friction is kinetic, mgsinθ-μmgcosθ=0. We do not know the coefficient of static friction, but even in case it is the same as that of the kinetic friction, the line of contact stays in rest, and the torque of gravity accelerates rotation about it. That rotation also moves the CM forward, the CM also accelerates, and a= Rα. Moving the CM will change the line of contact, the instantaneous axis will be placed forward. That is the process of "rolling without slipping".
You can determine the acceleration of the cylinder and from that also the force of friction. The acceleration is a=2/3 gsin(θ) and Fs=1/3 mgsin(θ). The maximum static friction is μmgcosθ=mgsinθ in our case, so Fs < μN. So the force of friction is less when rolling than the kinetic friction, when the cylinder is slipping. When rolling on a horizontal surface, the static friction is even zero. There are other effects causing rolling resistance which makes a rolling body stop at the end.

ehild

 

[Vibhor]

Thank you :)

So,the acceleration downward is constant , static friction acting on the cylinder is constant .But these results are derived from the assumption that a= Rα holds ?

How do we know that the condition v=Rω or a= Rα is satisfied all along the downward journey ?

 

[haruspex]

2) What is the cause of the initial speed of the cylinder downwards after it stops spinning ? The net force on the cylinder is always mgsinθ - μN i.e 0 ?

I assume you mean, the cause of the initial acceleration downwards.
As ehild wrote, when the surfaces are not slipping against each other, μ_sN is merely an upper limit on the frictional force . The actual frictional force, F, along the plane of contact at some instant is between -μ_sN and +μ_sN. When slipping it will be μ_kN <= μ_sN. All the time the cylinder is rotating in the uphill sense, it is just sufficient to balance the gravitational force. As soon as it stops spinning, it is not immediately clear what the value of the frictional force is.
To determine it, we allow that it might start rolling down. Let the angular acceleration be α, making the linear acceleration rα.
Torque about centre of cylinder: Iα = Fr
Acceleration down plane: mrα = mg sin(θ) - F.
Solve to find F and α. Check that 0 <= F <= μ_sN.

 

[ehild]

Thank you :)

So,the acceleration downward is constant , static friction acting on the cylinder is constant .But these results are derived from the assumption that a= Rα holds ?

How do we know that the condition v=Rω or a= Rα is satisfied all along the downward journey ?

a=Rα holds at the instant when the cylinder stops as both are zero. If the line of contact is in rest, the torque of gravity about the instantaneous axis is τ=mgsin(θ)*R. That torque causes angular acceleration α=τ/I. (I is with respect to the instantaneous axis now.) As the CM rotates about the instantaneous axis, and its distance from it is R, the linear acceleration of the CM is a=αR. Both a and α are constant and both the initial angular velocity and the initial linear velocity are zero, they are proportional to each other as time goes on: V=ωR all along the journey. That is rolling. We did not assume that relation, it came out from the condition of no slipping, that is, that the points of contact of the cylinder are in rest with respect to the incline. And no slipping is the consequence of the given coefficient of friction which prevents the cylinder starting to slip from rest.

It came out that the force of friction changed from that of kinetic friction to a much less value of static friction. It is sure that it happened gradually, but the process when the cylinder spun very slowly till it really stopped is not known. That process was governed by the forces between the surface molecules of the cylinder and those of the ground. It is beyond Mechanics.We do not know this process, we know only the outcome.

ehild

 

[ehild]

Torque about centre of cylinder: Iα = Fr
Acceleration down plane: m[STRIKE]r[/STRIKE]α = mg sin(θ) - F.
Solve to find F and α. Check that 0 <= F <= μ_sN.

there is a mistake in your equation.

ehild

 

[Vibhor]

To determine it, we allow that it might start rolling down. Let the angular acceleration be α, making the linear acceleration rα.
Torque about centre of cylinder: Iα = Fr
Acceleration down plane: mrα = mg sin(θ) - F.
Solve to find F and α. Check that 0 <= F <= μ_sN.

How did you assume rolling without slipping condition a = rα ?

Are you suggesting that we should assume this constraint and from this we find the static frictional force F and then prove that this F < μ_sN . Thereby concluding that since the frictional force required for rolling without slipping is less than μ_sN , rolling without slipping occurs .

But if we had obtained F > μ_sN , we could have argued that slipping does occur as friction is not sufficient .

Am I understanding it correctly ?

 

[ehild]

How did you assume rolling without slipping condition a = rα ?

Are you suggesting that we should assume this constraint and from this we find the static frictional force F and then prove that this F < μ_sN . Thereby concluding that since the frictional force required for rolling without slipping is less than μ_sN , rolling without slipping occurs .

But if we had obtained F > μ_sN , we could have argued that slipping does occur as friction is not sufficient .

Am I understanding it correctly ?

a=rα comes out from simple geometry.
Take a roll of paper and mark the end of the sheet. Keep this end fixed and make the cylinder of paper roll, while the sheet unwounding. When the mark returns to the original position, below the centre, the length of the removed sheet is equal to the displacement of the centre and equal to the circumference of the cross-sectional circle. You can check by wounding it back. The end will be at the mark. X=2Rπ. For an arbitrary angle of turn, X=Rθ. The first derivative is V=Rω, and the second derivative is a=Rα.

ehild

 

[Vibhor]

By now it seems as if I am the one who started this thread .

There is so much to learn here . Thanks ehild .

This question has raised another possibility that what would happen if instead of μ =tanθ as given , μ > tanθ .

Do you think if μ > tanθ ,then the cylinder moves up the incline after being placed on it ? Can the net force on the cylinder be upwards i.e frictional force F be greater than mgsinθ ?

 

[ehild]

This question has raised another possibility that what would happen if instead of μ =tanθ as given , μ > tanθ .

Do you think if μ > tanθ ,then the cylinder moves up the incline after being placed on it ? Can the net force on the cylinder be upwards i.e frictional force F be greater than mgsinθ ?

Yes, it can. The cylinder will gain upward velocity while its spinning slows down. At an instant V=Rω, so the rolling condition holds, the friction becomes static and gravity exceeding it. The cylinder will roll without slipping upward till the KE transforms completely to potential energy. From there on, the cylinder rolls downward.
Try it with a bicycle wheel...

ehild

 

[Vibhor]

At an instant V=Rω, so the rolling condition holds, and it will roll without slipping upward till the KE transforms completely to potential energy.
ehild

Is it right to say that in any situation whether the cylinder is moving up or moving down , once the cylinder achieves the no slipping condition V=Rω , it maintains this motion ? What I mean is that as soon as the cylinder rolls without slipping for the first time ,there is no possibility of slipping and the cylinder rolls without slipping thereafter .

Thank you for your patience . I am really gaining from this discussion.

 

[ehild]

Is it right to say that in any situation whether the cylinder is moving up or moving down , once the cylinder achieves the no slipping condition V=Rω , it maintains this motion ? What I mean is that as soon as the cylinder rolls without slipping for the first time ,there is no possibility of slipping and the cylinder rolls without slipping thereafter .

It looks so...

Thank you for your patience . I am really gaining from this discussion.

You are welcome. And accept my advice: Do experiments whenever possible. You learn a lot from them.

ehild