Time for falling down the incline (Rotating Solid Cylinder)

[ehild]

How did you assume rolling without slipping condition a = rα ?

Are you suggesting that we should assume this constraint and from this we find the static frictional force F and then prove that this F < μ_sN . Thereby concluding that since the frictional force required for rolling without slipping is less than μ_sN , rolling without slipping occurs .

But if we had obtained F > μ_sN , we could have argued that slipping does occur as friction is not sufficient .

Am I understanding it correctly ?

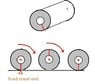
a=rα comes out from simple geometry.
Take a roll of paper and mark the end of the sheet. Keep this end fixed and make the cylinder of paper roll, while the sheet unwounding. When the mark returns to the original position, below the centre, the length of the removed sheet is equal to the displacement of the centre and equal to the circumference of the cross-sectional circle. You can check by wounding it back. The end will be at the mark. X=2Rπ. For an arbitrary angle of turn, X=Rθ. The first derivative is V=Rω, and the second derivative is a=Rα.

ehild

 

[Vibhor]

By now it seems as if I am the one who started this thread .

There is so much to learn here . Thanks ehild .

This question has raised another possibility that what would happen if instead of μ =tanθ as given , μ > tanθ .

Do you think if μ > tanθ ,then the cylinder moves up the incline after being placed on it ? Can the net force on the cylinder be upwards i.e frictional force F be greater than mgsinθ ?

 

[ehild]

This question has raised another possibility that what would happen if instead of μ =tanθ as given , μ > tanθ .

Do you think if μ > tanθ ,then the cylinder moves up the incline after being placed on it ? Can the net force on the cylinder be upwards i.e frictional force F be greater than mgsinθ ?

Yes, it can. The cylinder will gain upward velocity while its spinning slows down. At an instant V=Rω, so the rolling condition holds, the friction becomes static and gravity exceeding it. The cylinder will roll without slipping upward till the KE transforms completely to potential energy. From there on, the cylinder rolls downward.
Try it with a bicycle wheel...

ehild

 

[Vibhor]

At an instant V=Rω, so the rolling condition holds, and it will roll without slipping upward till the KE transforms completely to potential energy.
ehild

Is it right to say that in any situation whether the cylinder is moving up or moving down , once the cylinder achieves the no slipping condition V=Rω , it maintains this motion ? What I mean is that as soon as the cylinder rolls without slipping for the first time ,there is no possibility of slipping and the cylinder rolls without slipping thereafter .

Thank you for your patience . I am really gaining from this discussion.

 

[ehild]

Is it right to say that in any situation whether the cylinder is moving up or moving down , once the cylinder achieves the no slipping condition V=Rω , it maintains this motion ? What I mean is that as soon as the cylinder rolls without slipping for the first time ,there is no possibility of slipping and the cylinder rolls without slipping thereafter .

It looks so...

Thank you for your patience . I am really gaining from this discussion.

You are welcome. And accept my advice: Do experiments whenever possible. You learn a lot from them.

ehild

 

[haruspex]

there is a mistake in your equation.

ehild

That's an alpha (α), not an a.

 

[haruspex]

Are you suggesting that we should assume this constraint and from this we find the static frictional force F and then prove that this F < μ_sN . Thereby concluding that since the frictional force required for rolling without slipping is less than μ_sN , rolling without slipping occurs .

But if we had obtained F > μ_sN , we could have argued that slipping does occur as friction is not sufficient .

Am I understanding it correctly ?

Yes.