To find the relative velocity of the wind as seen from a car

[gnits]

Homework Statement

To find the relative velocity of the wind as seen from a car

Relevant Equations

Vab=Va-Vb

Could I please ask for any help with the following question:

Here's my attempt: (i and j are unit vectors in the directions of east and north respectively)

(apologies that LaTeX is simply not working for me, I'll label the angles in each case T and P as shown in my diagram)

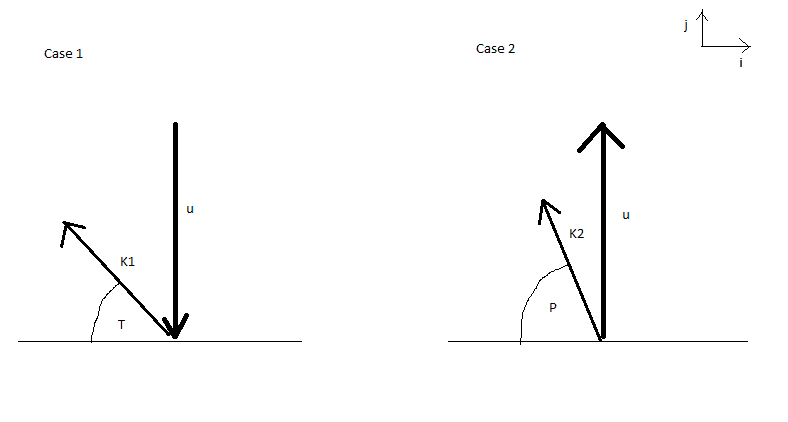
Let the velocity of the wind relative to the car be V_wc then:

V_wc = V_w - V_c

therefore V_w = V_wc + V_c

This is the true velocity of the wind.

In the first situation call the apparent magnitude of the wind's velocity K1 and in the second call it K2 then:

Case 1: V_w = -K1 * cos(T) i + ( K1 * sin(T) - u ) j

Case 2: V_w = -K2 * cos(P) i + ( K2 * sin(P) + u ) j

Now I can eliminate K1 and solve for K2, I get:

K2 = 2u / ( cos(P) tan(T) - sin(P) )

I can substitute this into the Case 2 equation for V_w to obtain:

V_w = ( -2u / [ tan(T) - tan(P) ] ) i + ( 2u / [ tan(T) tan(P) - 1 ] + u ) j

So this is the true velocity of the wind.

So now, for case 3 where the speed of the motorist is 2u heading north I need to find:

V_wc = V_w - V_c = ( -2u / [ tan(T) - tan(P) ] ) i + ( 2u / [ tan(T) tan(P) - 1 ] - u ) j

This leads to :

2 tan(w) = ( ( 2 / [ tan(T) tan(P) - 1 ] - 1 ) ) * (tan(T) - tan(P))

Which is not the desired answer.

Thanks for any help,
Mitch.

 

[gnits]

Just finished writing and posting this, then after all that effort, I found my mistake - an algebraic slip. The method works.