Topology: Connectedness and continuous functions

[perwiradua]

Could you please check the statement of the theorem and the proof? If the proof is more or less correct, can it be improved?

Theorem

Let

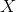be a topological space and

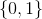be the discrete space.

The space

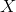is connected if and only if for any continuous functions

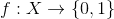, the function

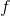is not onto.

Proof

Only if:

Suppose the space

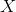is connected and suppose there exists a continuous function

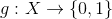which is onto. Then

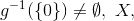since

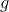is onto. Also since

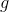is continuous,

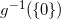is open and a proper subset of

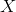. Let

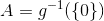and

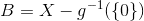. Both

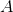and

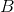are
proper and nonempty and clopen, and

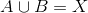. But this contradicts the connectedness of

.


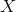If:

Conversely suppose for all functions

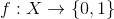, the function

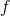is not onto. Suppose

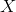is disconnected, say

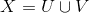where

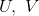are clopen and

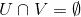. But then the function

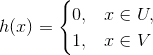
is continuous and onto.

 

[HallsofIvy]

Looks good but for (ii) you should say "Conversely, suppose for all continuous functions"