v54
- 6
- 0
Hi !
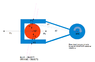
2 Objects turn at constant rotational velocity ω rd/s around axis noted "axis" on image (ω clockwise). An external system not drawn force the study to turn at ω rd/s if necessary. From blue object, forces F1 and F2 are applied to orange object. F1 = -F2 in vector.
I would like to know if orange object receive a torque and turn around its center of gravity "cg2" if I apply F1 and F2 forces ? I think if I want to apply a torque on orange object linear velocity must be the same of two points "A" and "B" where forces are applied. It's possible for a small distance dx I think. If I add a rotational velocity anticlockwise to orange object, it's possible to have the same velocity for each point. In this case F1/F2 forces on orange object will decrease potential energy, but this energy can be recover, no ?
Blue object receive a torque F2*d2-F1*d1 in the direction of rotation, so how the orange object cancel this torque ?
Thanks a lot for your reply !
2 Objects turn at constant rotational velocity ω rd/s around axis noted "axis" on image (ω clockwise). An external system not drawn force the study to turn at ω rd/s if necessary. From blue object, forces F1 and F2 are applied to orange object. F1 = -F2 in vector.
I would like to know if orange object receive a torque and turn around its center of gravity "cg2" if I apply F1 and F2 forces ? I think if I want to apply a torque on orange object linear velocity must be the same of two points "A" and "B" where forces are applied. It's possible for a small distance dx I think. If I add a rotational velocity anticlockwise to orange object, it's possible to have the same velocity for each point. In this case F1/F2 forces on orange object will decrease potential energy, but this energy can be recover, no ?
Blue object receive a torque F2*d2-F1*d1 in the direction of rotation, so how the orange object cancel this torque ?
Thanks a lot for your reply !
Attachments
Last edited: