- #1
NewtonFTW
- 4
- 0
Hi,
I have a few torque related questions,
But first, a basic one. Is torque Energy? Because Work=F.d (a force over a distance) measured in Joules (J). But then torque (measured in Newton per meter), sounds like it is also energy, and should also be measured in Joules, but it is not. What am I missing?
Please take a look at this diagram of a gearbox:
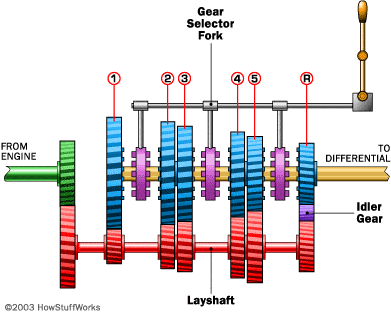
My confusion emanates from a formula I found online:
Torque_to_differential = Torque_from_engine * GearRatio
Where GearRatio is the ratio of the radius of the gear (gears are in blue) to the radius of the engine gear (shown in green here).
Now I am trying to understand why that is, and so I go back to the basic torque formula:
T = r x F ---> T= |r| * |F| * sin(theta) (If I am not mistaken)
But since in the case of a gear box, the torque vector, the r vector and the Force vector are all orthogonal, theta=0, hence:
|T| = |r| * |F|, therefore |F| = |T|/|r| (if I am not mistaken either...)
But here is my confusion, first of all, let's say a certain torque T is going through the Layshaft (in red). Does it mean that at each gear on the Layshaft the same amount of torque is communicated? It feels a bit counter intuitive...
My second questions goes back to the formula "Torque_to_differential = Torque_from_engine * GearRatio". If you look at the green gear that transmits power from the engine, my understanding of the way it communicates that torque to the first gear of the Layshaft is as follows:
Let's call Te the torque from the engine, and Re the radius of the green gear. I compute the force Fe = Te/Re (is that even right?). That force then is applied to the first gear of the Layshaft (left most red gear, with radius R=2Re, for example), generating a torque T=Fe*R = Te/Re*2Re = 2Te. Simply put, the gear doubles the amount of torque by having twice the radius of the driving gear. Is that correct so far?
But then things get confusing. I am assuming that the amount of torque Te that went through the first Layshaft gear, is the exact same as the one that goes through the second Layshaft gear (or radius Re/2, let's say). Is that right? Assuming it is, the force generated by that gear F=2Te/(Re/2)=4Te/Re. That force then generates a torque in the first gear of that gearbox (the large left-most blue gear, or radius R=3Re let's say) T=F*R = (4Te/Re)*(3Re)=12Te... This means that this mechanism, assuming prefect efficiency would yield 12 times the engine torque in first gear... which sound preposterous, and not at all in agreement with the "Torque_to_differential = Torque_from_engine * GearRatio" formula, which states that the torque in first gear should be simply 3 times the engine torque, due to the 3:1 gear ratio (first gear radius R is 3 times the radius of the engine's driving gear).
So in short, I know I am making a mistake somewhere, and I hope it will jump to you right away in my derivation.
Finally, on the issue of torque transmission through the layshaft, if I run a troque T through that shaft, how do I know what that torque is at each gear along that shaft? If I assume it is the exact same T at each gear, then it would imply something that seems wrong to me. Namely that the forces F1 at the first gear and F2 at the second one are generated from the same amount of energy... It would be like putting coins in a bag with two holes at the bottom, and having the exact same number of coins pouring out of both at the same time, effectively multiplying by two the number of coins you put in the bag. Clearly I don't understand what the physics are actually doing.
Thank you very much for your time and help,
-Serge
I have a few torque related questions,
But first, a basic one. Is torque Energy? Because Work=F.d (a force over a distance) measured in Joules (J). But then torque (measured in Newton per meter), sounds like it is also energy, and should also be measured in Joules, but it is not. What am I missing?
Please take a look at this diagram of a gearbox:
My confusion emanates from a formula I found online:
Torque_to_differential = Torque_from_engine * GearRatio
Where GearRatio is the ratio of the radius of the gear (gears are in blue) to the radius of the engine gear (shown in green here).
Now I am trying to understand why that is, and so I go back to the basic torque formula:
T = r x F ---> T= |r| * |F| * sin(theta) (If I am not mistaken)
But since in the case of a gear box, the torque vector, the r vector and the Force vector are all orthogonal, theta=0, hence:
|T| = |r| * |F|, therefore |F| = |T|/|r| (if I am not mistaken either...)
But here is my confusion, first of all, let's say a certain torque T is going through the Layshaft (in red). Does it mean that at each gear on the Layshaft the same amount of torque is communicated? It feels a bit counter intuitive...
My second questions goes back to the formula "Torque_to_differential = Torque_from_engine * GearRatio". If you look at the green gear that transmits power from the engine, my understanding of the way it communicates that torque to the first gear of the Layshaft is as follows:
Let's call Te the torque from the engine, and Re the radius of the green gear. I compute the force Fe = Te/Re (is that even right?). That force then is applied to the first gear of the Layshaft (left most red gear, with radius R=2Re, for example), generating a torque T=Fe*R = Te/Re*2Re = 2Te. Simply put, the gear doubles the amount of torque by having twice the radius of the driving gear. Is that correct so far?
But then things get confusing. I am assuming that the amount of torque Te that went through the first Layshaft gear, is the exact same as the one that goes through the second Layshaft gear (or radius Re/2, let's say). Is that right? Assuming it is, the force generated by that gear F=2Te/(Re/2)=4Te/Re. That force then generates a torque in the first gear of that gearbox (the large left-most blue gear, or radius R=3Re let's say) T=F*R = (4Te/Re)*(3Re)=12Te... This means that this mechanism, assuming prefect efficiency would yield 12 times the engine torque in first gear... which sound preposterous, and not at all in agreement with the "Torque_to_differential = Torque_from_engine * GearRatio" formula, which states that the torque in first gear should be simply 3 times the engine torque, due to the 3:1 gear ratio (first gear radius R is 3 times the radius of the engine's driving gear).
So in short, I know I am making a mistake somewhere, and I hope it will jump to you right away in my derivation.
Finally, on the issue of torque transmission through the layshaft, if I run a troque T through that shaft, how do I know what that torque is at each gear along that shaft? If I assume it is the exact same T at each gear, then it would imply something that seems wrong to me. Namely that the forces F1 at the first gear and F2 at the second one are generated from the same amount of energy... It would be like putting coins in a bag with two holes at the bottom, and having the exact same number of coins pouring out of both at the same time, effectively multiplying by two the number of coins you put in the bag. Clearly I don't understand what the physics are actually doing.
Thank you very much for your time and help,
-Serge