Jan Grossmann
- 3
- 0
Hi all,
I am currently working on a creating a mathematical model of a longboard and am in need of advice. The pictures describe the sitaution.
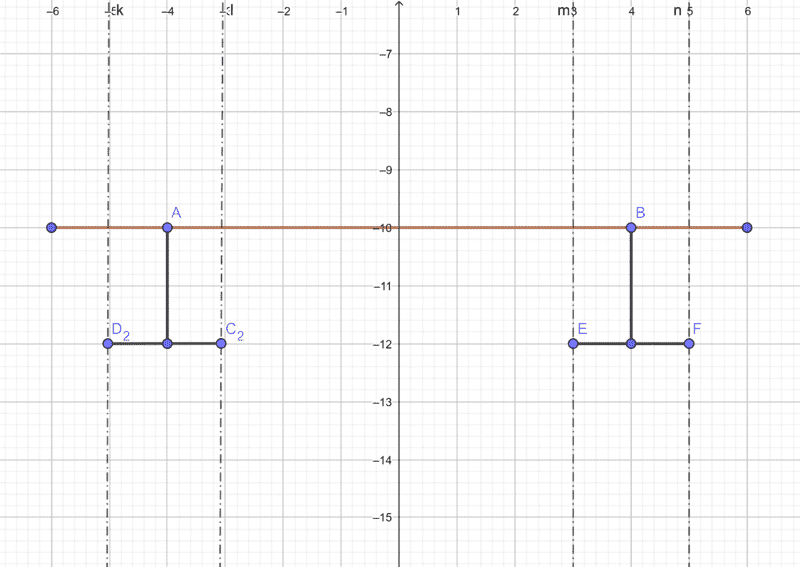
Side view
Top view
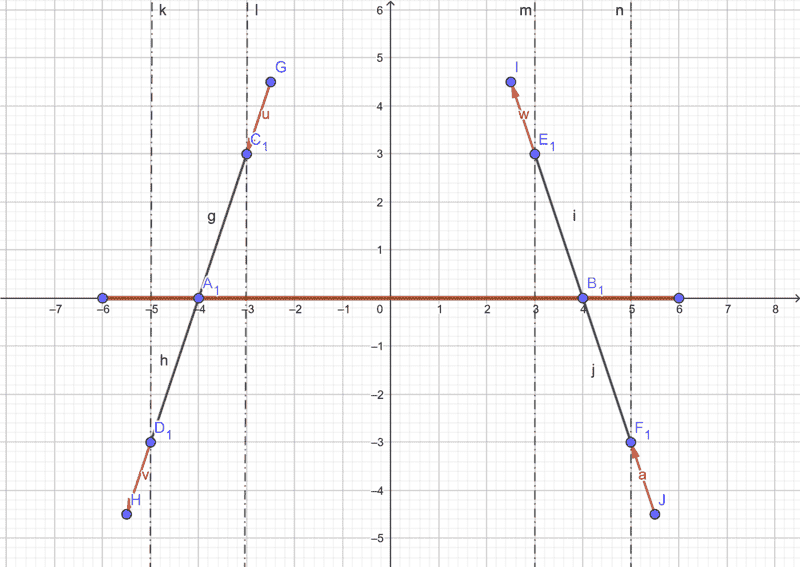
Back view
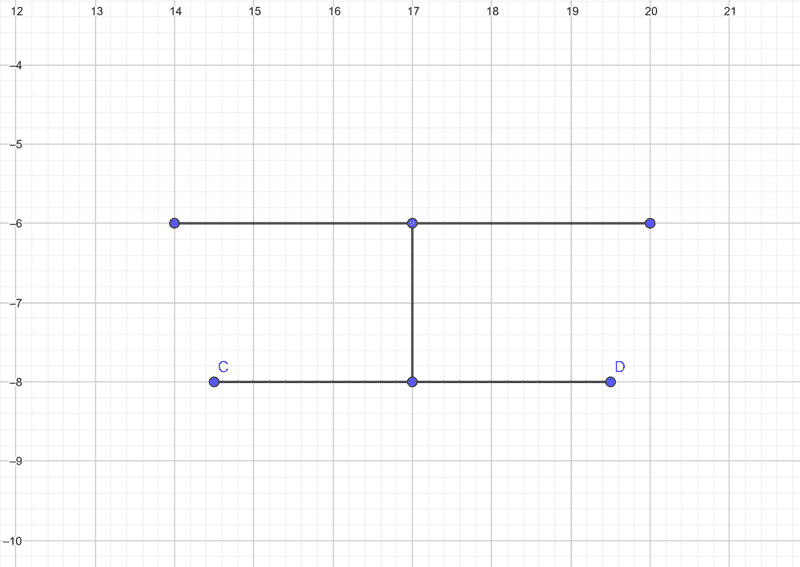
The pictures depict a simplified longboard - the brown line is the deck and the black lines represent the trucks - at an angle because the longboard is turning. Point C,D,E,F are where the wheels are. The center of gravity and rotation lies at the coordinantes 0,0, e.i. in the middle of the deck on line A,B. Now my question regards the vectors u,v,w,a - these are force vectors generated by the wheels in a turn. These forces generate a torque about the COR in the axis perpendicular to line CD. I need to know the torque in the axis on line AB. Can I calculate the torque simply by transfroming the force vectors into the axis perpendicular to AB and using these transformed forces to calculate, or is this approach not correct? Thank you in adavance.
John
I am currently working on a creating a mathematical model of a longboard and am in need of advice. The pictures describe the sitaution.
Side view
Top view
Back view
The pictures depict a simplified longboard - the brown line is the deck and the black lines represent the trucks - at an angle because the longboard is turning. Point C,D,E,F are where the wheels are. The center of gravity and rotation lies at the coordinantes 0,0, e.i. in the middle of the deck on line A,B. Now my question regards the vectors u,v,w,a - these are force vectors generated by the wheels in a turn. These forces generate a torque about the COR in the axis perpendicular to line CD. I need to know the torque in the axis on line AB. Can I calculate the torque simply by transfroming the force vectors into the axis perpendicular to AB and using these transformed forces to calculate, or is this approach not correct? Thank you in adavance.
John