asdasdasd
- 3
- 0
Torque/Translational and Rotational Equilibrium
I was given this problem as a quiz in class. Unfortunately, I did not finish it. I decided to try it at home as I need the practice.
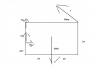
Sorry for the crudely drawn image.
http://image.bayimg.com/lajgkaabb.jpg
Find: T, T_2y, T_3y, T_3x given T_2y = T_3y and the object is in translational and rotational equilibrium.
Figure of problem also attached.
Don't think there are any.
Sum of all forces is zero.
\Sigma x = T_3x + -T\cos30^\circ = 0
\Sigma y = 2T_2y + T\sin30^\circ - 500N = 0
Sum of torque is zero.
\Sigma\Gamma = -(4m)(2T_2y) + (1.75m)T_3x + (2m)(500N)
Substitution time?
T_3x = T\cos30^\circ
T_2y = \frac{500N - T\sin30^\circ}{2}
0N = -(4m)(500N - T\sin30^\circ) + (1.75m)(T\cos30^\circ) + 1000N
0N = -1000N + 3.516T
Proposed values
T = 284.414N
T_3x = 246.31N
T_2y = T_3y = 178.896N
I just want to know if I did this correctly. If not, I would greatly appreciated any help. Thanks for taking the time to read this.
I was given this problem as a quiz in class. Unfortunately, I did not finish it. I decided to try it at home as I need the practice.
Homework Statement
Sorry for the crudely drawn image.
http://image.bayimg.com/lajgkaabb.jpg
Find: T, T_2y, T_3y, T_3x given T_2y = T_3y and the object is in translational and rotational equilibrium.
Figure of problem also attached.
Homework Equations
Don't think there are any.
The Attempt at a Solution
Sum of all forces is zero.
\Sigma x = T_3x + -T\cos30^\circ = 0
\Sigma y = 2T_2y + T\sin30^\circ - 500N = 0
Sum of torque is zero.
\Sigma\Gamma = -(4m)(2T_2y) + (1.75m)T_3x + (2m)(500N)
Substitution time?
T_3x = T\cos30^\circ
T_2y = \frac{500N - T\sin30^\circ}{2}
0N = -(4m)(500N - T\sin30^\circ) + (1.75m)(T\cos30^\circ) + 1000N
0N = -1000N + 3.516T
Proposed values
T = 284.414N
T_3x = 246.31N
T_2y = T_3y = 178.896N
I just want to know if I did this correctly. If not, I would greatly appreciated any help. Thanks for taking the time to read this.
Attachments
Last edited by a moderator: