denfaro
- 8
- 2
- Homework Statement
- Almost Done.
- Relevant Equations
- T=p*e
Hi I am confused in this question. What Can I do after the steps in second photo?
Join the discussion
Ask a follow-up here, or get your own question answered by working scientists, mathematicians and engineers — people, not an autocomplete.
Real named experts · corrections over time · the nuance an AI answer skips
2 replies · 1K views
- 16,219
- 4,934
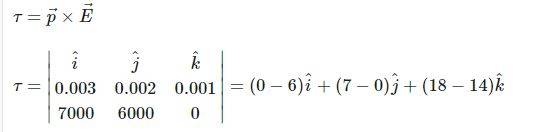
I think you are done: you have calculated the torque, which is what the exercise asked...denfaro said:
- 16,043
- 9,259
##\dots## except for the units.BvU said:
