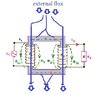
I have run a number of experiments, but none has shed any light on the matter. I have this set of three 2-winding transformers side-by-side, and when I apply a 1 kHz field on them the current through their windings increases, independent of other currents.
The transformer directly under the antenna's center shows the strongest current, which discards the hypothesis that the field is getting coupled to something other than the transformers, like another loop in the circuit.
When I apply fields with frequencies a little different the currents are smaller, and if I graph current vs frequency I get a Lorentzian curve. This suggests there's a resonance in an RCL circuit somewhere, but I've taken away the decoupling caps and the effect persists. There are no other reactive components that can form a resonance together with the transformer's coils.
Applying the field sideways doesn't create any current. It's only when the field is entering in the direction of the coils. That's why I was asking if it is theoretically possible for an external field to induce currents in the same way the primary coil induces a current in the secondary coil, which according to my calculations it doesn't. This is how I got to that conclusion, parting from a basic 2-solenoid transformer like you see in high-school physics, like this:
plus a downward-pointing uniform AC magnetic field:
The external flux is going to induce a current in the primary equal to
$$ I = \frac{\Phi_E}{N_1} $$
and in a sense contrary to the incoming current I1 (assuming the first coil is winded clockwise as seen from above). The total current through the primary coil will therefore create a magnetic flux equal to:
$$ \Phi_1 = N_1 ( I_1 - \frac{\Phi_E}{N_1} ) = N_1 I_1 - \Phi_E $$
The flux going into the secondary coil is the flux generated by the primary coil plus the external flux, so
$$ \Phi_2 = N_1 I_1 - \Phi_E + \Phi_E = N_1 I_1 $$
And therefore the currents will get transformed as if the external field wasn't there, i.e. a current will appear in the secondary coil that will create the Φ
2L flux equal but opposite to Φ
2:
$$ I_2 N_2 = N_1 I_1$$
$$ I_2 = \frac{N_1}{N_2} I_1 $$
Of course I haven't put any thought into whether the external field might be saturating the core. Would this effect be frequency-dependent?
Thank you for your time. I understand if the rules mean you'll only be helping me with the theoretical question and not with the practical side of what to do from there.