Java Transforming Infix to Postfix in Java: Solving Arithmetic Expressions with RPN

[muna580]

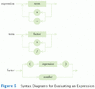
I am creating a class that will transform a basic arithmetic expression from infix to postfix (Reverse Polish Notation (RPN)). Then after then, it will evaluate the postfix expression and give the answer.

I have having a little trouble with the operators (+,-,/,0*, and %). Like, I have to create a method called hasHigherPrecedence(char c1, char c2), which returns a boolean saying where c1 has a higher precedence than c2. But I don't really know hwo to create this method. Can someone help me.

 

[Hurkyl]

Forget programming for a moment.

If I asked you to tell me which of "+" or "*" had higher precedence, what would you do to figure it out?

What if you had to teach a 10-year hold how to figure it out? How would you do that?

 

[muna580]

Umm, I think this is the precedence order from highest to lowest: * / + -. Where does the % go?

 

[verty]

This is homework or an assignment, right?

 

[haki]

Create a syntax diagram and make code to follow it.

http://www.horstmann.com/bigj2/slides/slides18.zip

here is the cleanest program to evaluate an arithmetic expression I have ever seen. Evaluator.java, it took me some time to figure it out exactly but it is worft it.

 

[Energex42]

You have to definitively look up the operator's precedence orders. Usually this piece of information can be found in the chapter that describe integer operators. Certain operators have identical precedence orders. I would assign an integer precedence level value to each operator.

 

[twisting_edge]

Umm, I think this is the precedence order from highest to lowest: * / + -. Where does the % go?

If you mean the modulus operator in C, it has the same precedence as the '/' operator.

Good luck with the RPN, I might add. I wrote a set of C functions to do that parsing for me once. I'm still not happy with it, and have sunk weeks into it over the course of years (it probably didn't help that I was tryign to do something slightly different with it every time I reopened that particular can of worms).

The cheap and sleazy fix is to get the entire formula into a string, then build a binary tree from it by simply splitting the string on each precedence, with same same precedence from left to right, then splitting each substring on the next precedence, etc. That actually works pretty well. Matched delimiters affecting parsing (e.g., [], (), and "") are messy but not too bad.

The problem arises when you have multiline input. Cheap and sleazy no longer works. Then you have to do it the right way with a stack. That's when it gets messy.

Once you've got the tree, spitting out the RPN is obviously trivial.

 

[haki]

I also had to write the same program in C (parse infix arithmetic expression and print postfix and prefix), I first wrote it in Java took me less than 30 mins, and then I tried to write it in C it took me about 7 hours to do it, I spend 3,5 hours searching for a bug it turned out that I allocated a struct wrongly, I could never have done such a mistake in Java, anyway, I am very pleased with my C program and specially with Java, one way is to do some elaborate substring work but that is a mess, there is an alternative way, you can do it recursively. Make a syntax diagram and follow it recursively, very hard to make a mistake then. Something like that

 /**
      Evaluates the expression.
      @return the value of the expression.
   */
   public Node getExpressionValue()
   {
      Node value = getTermValue();
      boolean done = false;
      while (!done)
      {
         String next = tokenizer.peekToken();
         if ("+".equals(next) || "-".equals(next))
         {
            tokenizer.nextToken(); // Discard "+" or "-"
            Node value2 = getTermValue();
            if ("+".equals(next)) value = new Node("+", value, value2);
            else value = new Node("-", value, value2);
         }
         else done = true;
      }
      return value;
   }

   /**
      Evaluates the next term found in the expression.
      @return the value of the term
   */
   public Node getTermValue()
   {
      Node value = getFactorValue();
      boolean done = false;
      while (!done)
      {
         String next = tokenizer.peekToken();
         if ("*".equals(next) || "/".equals(next))
         {
            tokenizer.nextToken();
            Node value2 = getFactorValue();
            if ("*".equals(next)) value = new Node("*", value, value2);
            else value = new Node("/", value, value2);
         }
         else done = true;
      }
      return value;
   }

   /**
      Evaluates the next factor found in the expression.
      @return the value of the factor
   */
   public Node getFactorValue()
   {
      Node value;
      String next = tokenizer.peekToken();
      if ("(".equals(next))
      {
         tokenizer.nextToken(); // Discard "("
         value = getExpressionValue();
         tokenizer.nextToken(); // Discard ")"
      }
      else
         value = new Node(tokenizer.nextToken());
      return value;
   }