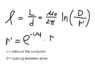The location matters because the mutual inductance and capacitance changes with regard to the orientation of the conductors in space (or in the ground). The mutual inductance of three parallel conductors is different than the mutual inductance of 3 conductors oriented equilaterally. By this, Transposing will keep the impedance close enough to being equal on each phase. Transposing one of the phases will also result in one of the phases being slightly longer than the other two, affecting the self-inductance (very) slightly (not really considered).
If you're taking your Electromagnetics class now it would be a good exercise to create a general mathematical model for the effect each Transposing scheme has on a circuit's inductance and capacitance. Also, make some changes to the GMD (Geometric mean distance) to help solidify concepts. I'll do it as well once I get some spare time. I'll post it here when (and if) I get it done.Every conductor will have a self-inductance and shunt-capacitance to the return. Every grouping of conductors will have a mutual inductance and capacitance. Every conductor will have a resistance, though usually ignored at high voltages (lower currents). Resistance of a conductor does not depend on magnetic or electric field phenomena so has no change when sharing close proximity with other conductors.
The impedance of a wire is derived from the conductance of it's material, construction details (cross-section, etc.), and it's behavior when exposed to changing magnetic and electric fields (also affected by material and construction details, but also including frequency). So:
Z=R+iX and
X=i2π⋅f⋅L or
X=i2π⋅f⋅(1/C). (Where Inductance (L) and Capacitance (C) describe the conductor's behavior in response to changing Magnetic fields and changing Electric fields respectively). Understanding that, it should follow that the reactive part of impedance will change with orientation of conductors in space relative to other conductors and the phase conductor's length; whereas, the resistive part of the impedance will change only with length.I think what you meant is, "how could a non-perfect triangle (equilateral?) make the impedances balanced." (I say this since, given how you phrased your original questions, the answer should have been clear to you at that point. Correct me if I'm wrong.). As mentioned, shunt capacitance and mutual inductance both change with the orientation of conductors. Put three conductors in a line. Calculate mutual inductance and capacitance. Place them then in an equilateral triangle. Recalculate. Place them in a right triangle. Recalculate. What changed? Increase the distances between conductors. Recalculate everything. What changed? Decrease the distances between conductors. Recalculate everything. What changed?
(
@anorlunda ,
@berkeman ,
@jim hardy,
@Baluncore please correct me where I've misspoken)