Treating Mass as a perturbation

[Sekonda]

Hello again,

I also have another question, somewhat related to my previous, on the topic of the Klein-Gordon equation but treating the mass as a perturbation.

The feynman diagram shows the particular interaction:

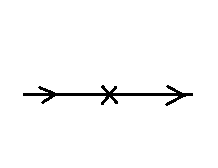
I believe the cross is the point of interaction via the perturbation (the mass), we model the perturbation:

\delta V=m^2

and subsequently use this in the calculation for the transition amplitude, we use plane-wave solutions of the ingoing and outgoing states.

Alike to my previous question, I'm not really sure what this means to model some potential as a mass? Can anyone explain why we do this and maybe exactly what is happening in this particular feynman diagram?

I can try to embelish if needs be, please tell me if there are any inconsistencies or errors I have made in my explanation of my problem!

Thanks,
SK

 

[Sekonda]

The self energy of a particle is the contribution to the particles energy due to interactions with the system. Considering we are dealing with a relativistic particle, is this self energy the invariant mass term in the relativistic energy-momentum relation and thus can be treated as the perturbation/potential of the system or interaction?

 

[andrien]

self energy contribution is repalced by a change in mass which is attributed to it.It helps to redefine the masses and charges by renormalized charge and mass.you can see sakurai 'advanced quantum mechanics' for why this can be treated as a mass change.