- #1
Jhenrique
- 685
- 4
Is it possible to formulate the second derivate trough of a tree diagram, as we do with a first derivative? If yes, how do it?
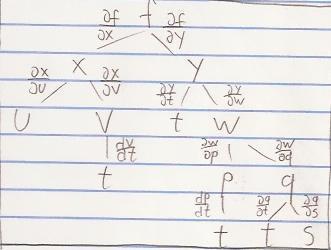
[tex]\frac{\partial f}{\partial t}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial v}\frac{\partial v}{\partial t}+\frac{\partial f}{\partial y}\left(\frac{\partial y}{\partial t}+\frac{\partial y}{\partial w}\left(\frac{\partial w}{\partial q}\frac{\partial q}{\partial t} + \frac{\partial w}{\partial p}\frac{\partial p}{\partial t}\right )\right )[/tex]
Edit: example: suppose you need to make the second partial derivative ∂²f/∂s∂t
[tex]\frac{\partial f}{\partial t}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial v}\frac{\partial v}{\partial t}+\frac{\partial f}{\partial y}\left(\frac{\partial y}{\partial t}+\frac{\partial y}{\partial w}\left(\frac{\partial w}{\partial q}\frac{\partial q}{\partial t} + \frac{\partial w}{\partial p}\frac{\partial p}{\partial t}\right )\right )[/tex]
Edit: example: suppose you need to make the second partial derivative ∂²f/∂s∂t
