bigbk92
- 10
- 0
Vector A and vector B are expressed in component form.
A = [2.32,-5.16,7.88]
B = [-1.12,3.45,-12.8]
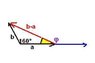
The standard arrow representation of these vectors and that of can be arranged to form a triangle in a plane that represents the geometric equivalent of the subtraction operation. The following items refer to this triangle.
(a) Please state, to three significant figures, the three angles of the triangle.
(b) Please express, in component form to three significant figures, a vector of magnitude 5.00 units that is perpendicular to the plane of the triangle.
(c) Please express, in component form to three significant figures, a second vector of magnitude 5.00 units that is perpendicular to the plane of the triangle.
I think the way I am supposed to appraoch this problem is to make a third vector B-A which will connect to B and A to make a triangle. So I found B-A to be [-3.44,8.61,-20.68].
Then I found the angle between A and B by using the dot product(equal to -121.3) and found the angle to be 160 degrees. I did the same thing to find the anggle between A and B-A but the angle was 169 degrees. So this is not a triangle as the angles do not add to 180 degrees.
Can someone help me figure out where i went wrong and how to approach this problem?
A = [2.32,-5.16,7.88]
B = [-1.12,3.45,-12.8]
The standard arrow representation of these vectors and that of can be arranged to form a triangle in a plane that represents the geometric equivalent of the subtraction operation. The following items refer to this triangle.
(a) Please state, to three significant figures, the three angles of the triangle.
(b) Please express, in component form to three significant figures, a vector of magnitude 5.00 units that is perpendicular to the plane of the triangle.
(c) Please express, in component form to three significant figures, a second vector of magnitude 5.00 units that is perpendicular to the plane of the triangle.
I think the way I am supposed to appraoch this problem is to make a third vector B-A which will connect to B and A to make a triangle. So I found B-A to be [-3.44,8.61,-20.68].
Then I found the angle between A and B by using the dot product(equal to -121.3) and found the angle to be 160 degrees. I did the same thing to find the anggle between A and B-A but the angle was 169 degrees. So this is not a triangle as the angles do not add to 180 degrees.
Can someone help me figure out where i went wrong and how to approach this problem?