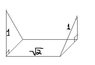
- #1
Natasha1
- 493
- 9
I was wondering whether someone could come up with the proof of this exercise I set myself:
We have four different types of triangles to play with (unlimited amounts of each):
one triangle which has 3 sides of length 1
one triangle which has 2 sides of length 1 and one of length square root 2
one triangle which has 2 sides of length square root 2 and one of side length 1
one triangle which has 3 sides of length square root 2
When I assumble 4 triangles together, what is the maximum amount of irregular tetrahedron (3-D shape) I can form. And what is the proof to make sure I have found the maximum?
My answer so far is:
Using:
4 triangles the same shape ----- you can make 2 irregular tetrahedrons.
3 triangles the same shape----- you can make 2 irregular tetrahedrons.
2 the same + 2 same (but different to the 2 others) ---- you can make 1 irregular tetrahedron.
2 the same + 2 different --- you can make 3 irregular tetrahedrons (I'm not sure on this one)
0 different ---- obviously 0 irregular tetrahedron.
Does this make any sense?
We have four different types of triangles to play with (unlimited amounts of each):
one triangle which has 3 sides of length 1
one triangle which has 2 sides of length 1 and one of length square root 2
one triangle which has 2 sides of length square root 2 and one of side length 1
one triangle which has 3 sides of length square root 2
When I assumble 4 triangles together, what is the maximum amount of irregular tetrahedron (3-D shape) I can form. And what is the proof to make sure I have found the maximum?
My answer so far is:
Using:
4 triangles the same shape ----- you can make 2 irregular tetrahedrons.
3 triangles the same shape----- you can make 2 irregular tetrahedrons.
2 the same + 2 same (but different to the 2 others) ---- you can make 1 irregular tetrahedron.
2 the same + 2 different --- you can make 3 irregular tetrahedrons (I'm not sure on this one)
0 different ---- obviously 0 irregular tetrahedron.
Does this make any sense?
Last edited: