Triangular Matrix RIngs .... Lam, Proposition 1.17

[Math Amateur]

I am reading T. Y. Lam's book, "A First Course in Noncommutative Rings" (Second Edition) and am currently focussed on Section 1:Basic Terminology and Examples ...

I need help with Part (1) of Proposition 1.17 ... ...

Proposition 1.17 (together with related material from Example 1.14 reads as follows:

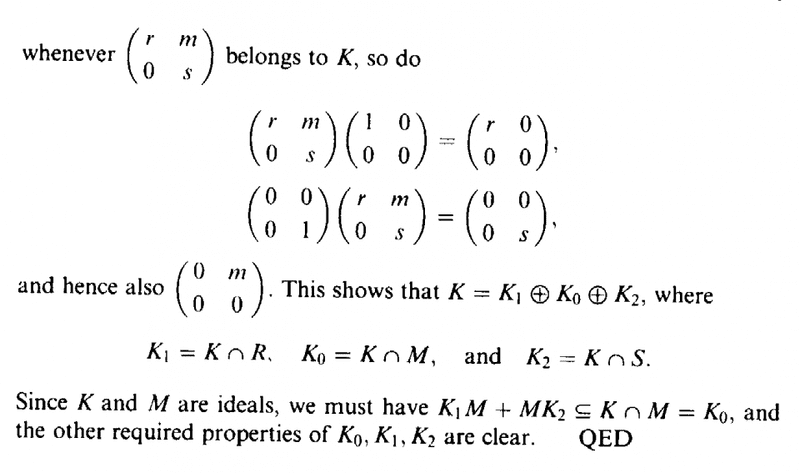
Can someone please help me to prove Part (1) of the proposition ... that is that $I_1 \oplus I_2$ is a left ideal of A ... ...

Help will be much appreciated ...

Peter

 

[micromass]

What did you try? What is it that you need to prove? What is the definition of a left ideal? What happens when you try to prove this definition in this case?

 

[Math Amateur]

I have been reflecting on the problem I posed ... here is my 'solution' ... Note: I am quite unsure of this ...

Problem ... Let $I = I_1 \oplus I_2$ where $I_1$ is a left ideal of $S$ and $I_2$ is a left submodule of $R \oplus M$ ...

Show $I$ is a left ideal of $A$
Let $a \in I$, then there exists $a_1 \in I_1$ and $a_2 \in I_2$ such that $a = (a_1, a_2) \in I$

[ ... ... actually $a_2 = (c_1, c_2) \in R \oplus M$ but we ignore this complication in order to keep notation simple ... ]Similarly let $b \in I$ so $b = (b_1, b_2) \in I$ ... ...
Now ... if $I$ is a left ideal then

$a, b \in I \ \Longrightarrow \ a - b \in I$

and

$r \in A$ and $a \in I \ \Longrightarrow \ ra \in I$--------------------------------------------------------------------------------------------------------------------------------------------

To show $a, b \in I \ \Longrightarrow \ a - b \in I$
Let $a,b \in I$

then $a - b = (a_1, a_2) - (b_1, b_2)$ where $a_1, b_1 \in S$ and $a_2, b_2 \in R \oplus M$

so, $a - b = (a_1 - b_1, a_2 - b_2)$

But ... $a_1 - b_1 \in I_1$ since $I_1$ is an ideal in $S$

and ... $a_2 - b_2 \in I_2$ since $I_2$ is a left sub-module of $A$

hence $(a_1 - b_1, a_2 - b_2) = a - b \in I$------------------------------------------------------------------------------------------------------------------------------------To show $r \in A \text{ and } a \in I \ \Longrightarrow \ ra \in I$
Now ... $r \in A$ and $a \in I \ \Longrightarrow \ ra = r(a_1, a_2) = (ra_1, ra_2)$ [I hope this is correct!]

But $ra_1 \in I_1$ since $I_1$ is a left ideal ...

and $ra_2 \in I_2$ since $I_2$ is a left $R$-submodule ...

Hence $(ra_1, ra_2) = ra \in I$-------------------------------------------------------------------------------------------------------------------------------------

The above shows that I is a left ideal ... I think ...

Comments critiquing the above analysis and/or pointing out errors are more than welcome ...

Peter

 

[fresh_42]

I have been reflecting on the problem I posed ... here is my 'solution' ... Note: I am quite unsure of this ...

Problem ... Let $I = I_1 \oplus I_2$ where $I_1$ is a left ideal of $S$ and $I_2$ is a left submodule of $R \oplus M$ ...

Show $I$ is a left ideal of $A$
Let $a \in I$, then there exists $a_1 \in I_1$ and $a_2 \in I_2$ such that $a = (a_1, a_2) \in I$

[ ... ... actually $a_2 = (c_1, c_2) \in R \oplus M$ but we ignore this complication in order to keep notation simple ... ]Similarly let $b \in I$ so $b = (b_1, b_2) \in I$ ... ...
Now ... if $I$ is a left ideal then

$a, b \in I \ \Longrightarrow \ a - b \in I$

and

$r \in A$ and $a \in I \ \Longrightarrow \ ra \in I$--------------------------------------------------------------------------------------------------------------------------------------------

To show $a, b \in I \ \Longrightarrow \ a - b \in I$
Let $a,b \in I$

then $a - b = (a_1, a_2) - (b_1, b_2)$ where $a_1, b_1 \in S$ and $a_2, b_2 \in R \oplus M$

so, $a - b = (a_1 - b_1, a_2 - b_2)$

But ... $a_1 - b_1 \in I_1$ since $I_1$ is an ideal in $S$

and ... $a_2 - b_2 \in I_2$ since $I_2$ is a left sub-module of $A$

hence $(a_1 - b_1, a_2 - b_2) = a - b \in I$------------------------------------------------------------------------------------------------------------------------------------To show $r \in A \text{ and } a \in I \ \Longrightarrow \ ra \in I$
Now ... $r \in A$ and $a \in I \ \Longrightarrow \ ra = r(a_1, a_2) = (ra_1, ra_2)$ [I hope this is correct!]

But $ra_1 \in I_1$ since $I_1$ is a left ideal ...

and $ra_2 \in I_2$ since $I_2$ is a left $R$-submodule ...

Hence $(ra_1, ra_2) = ra \in I$-------------------------------------------------------------------------------------------------------------------------------------

The above shows that I is a left ideal ... I think ...

Comments critiquing the above analysis and/or pointing out errors are more than welcome ...

Peter

Yes, I don't see anything wrong. And, yes, $r(a_1,a_2) = (ra_1,ra_2)$. Remember that you wrote $a_1 + a_2$ as $(a_1,a_2)$.
I would have used a more general approach, i.e. not with single elements, but it's been a good exercise though.
Addition is clear, because addition is component-wise and the components are closed under addition (ideal and module).
And multiplication goes
$$ \begin{bmatrix}R && M \\ 0 && S\end{bmatrix} \cdot \begin{bmatrix} I_1 \\ I_2\end{bmatrix}=\begin{bmatrix}RI_1 + MI_2 \\ S I_2\end{bmatrix} \subseteq \begin{bmatrix}I_1 + I_1 \\ I_2 \end{bmatrix}\subseteq \begin{bmatrix}I_1 \\ I_2 \end{bmatrix}$$
I guess this is also used for the converse direction. Comparison of the second component (plus a similar equation for addition) gives you immediately that $I_2 \subseteq S$ has to be a left ideal, so only the first component with a few conditions more needs to be examined.

 

[Math Amateur]

Sorry for late reply, fresh_42 ... been traveling ...

So grateful for your help on this matter ...

Reflecting on what you have said ...

Peter

 

[fresh_42]

You're welcome. Peter.

 

[Math Amateur]

Yes, I don't see anything wrong. And, yes, $r(a_1,a_2) = (ra_1,ra_2)$. Remember that you wrote $a_1 + a_2$ as $(a_1,a_2)$.
I would have used a more general approach, i.e. not with single elements, but it's been a good exercise though.
Addition is clear, because addition is component-wise and the components are closed under addition (ideal and module).
And multiplication goes
$$ \begin{bmatrix}R && M \\ 0 && S\end{bmatrix} \cdot \begin{bmatrix} I_1 \\ I_2\end{bmatrix}=\begin{bmatrix}RI_1 + MI_2 \\ S I_2\end{bmatrix} \subseteq \begin{bmatrix}I_1 + I_1 \\ I_2 \end{bmatrix}\subseteq \begin{bmatrix}I_1 \\ I_2 \end{bmatrix}$$
I guess this is also used for the converse direction. Comparison of the second component (plus a similar equation for addition) gives you immediately that $I_2 \subseteq S$ has to be a left ideal, so only the first component with a few conditions more needs to be examined.

Yes, I don't see anything wrong. And, yes, $r(a_1,a_2) = (ra_1,ra_2)$. Remember that you wrote $a_1 + a_2$ as $(a_1,a_2)$.
I would have used a more general approach, i.e. not with single elements, but it's been a good exercise though.
Addition is clear, because addition is component-wise and the components are closed under addition (ideal and module).
And multiplication goes
$$ \begin{bmatrix}R && M \\ 0 && S\end{bmatrix} \cdot \begin{bmatrix} I_1 \\ I_2\end{bmatrix}=\begin{bmatrix}RI_1 + MI_2 \\ S I_2\end{bmatrix} \subseteq \begin{bmatrix}I_1 + I_1 \\ I_2 \end{bmatrix}\subseteq \begin{bmatrix}I_1 \\ I_2 \end{bmatrix}$$
I guess this is also used for the converse direction. Comparison of the second component (plus a similar equation for addition) gives you immediately that $I_2 \subseteq S$ has to be a left ideal, so only the first component with a few conditions more needs to be examined.

Thanks again for your help, fresh_42 ...

You write:

"... ... And, yes, $r(a_1,a_2) = (ra_1,ra_2)$. Remember that you wrote $a_1 + a_2$ as $(a_1,a_2)$. ... ... My justification for doing this was that the direct sum and the direct product are isomorphic for finite cases in rings/modules ... is this correct?You also wrote:

"... ... I would have used a more general approach, i.e. not with single elements ... ...

Can you give me an idea of your more general approach ... ?

Peter

 

[fresh_42]

You write:

"... ... And, yes, $r(a_1,a_2) = (ra_1,ra_2)$. Remember that you wrote $a_1 + a_2$ as $(a_1,a_2)$. ... ...My justification for doing this was that the direct sum and the direct product are isomorphic for finite cases in rings/modules ... is this correct?

Yes, it is correct.

The difference between direct products and direct sums is that we consider projections $p_\nu : \Pi_{\mu \in I} M_\mu \twoheadrightarrow M_\nu$ in the case of direct products and injections $i_\nu : M_\nu \rightarrowtail \Sigma_{\mu \in I} M_\mu$ in the case of direct sums to define them. So it is more of a categorical difference.

There is nothing wrong with your notation. I simply mentioned it, because written as a sum, $r(a_1,a_2) = (ra_1,ra_2)$ becomes more obvious.

"... ... I would have used a more general approach, i.e. not with single elements ... ...

Can you give me an idea of your more general approach ... ?

General approach was a bit high-flown. I haven't been lucky with the wording but couldn't find an alternative quickly.
I simply wanted to say, that it's enough to work with the entire sets instead of with single elements. But your right that the latter is more rigor.
The notation with sets is likely a sloppiness I got used to through the years.
$R I \subseteq I$ is simply shorter than $\forall r \in R \; \forall i \in I \Rightarrow r \cdot i \in I$ and likewise for addition, or as in our case the matrix multiplication. It spares all the $Let \; r \in R \, , \, s \in S \, , \, m \in M \, , \, i_1 \in I_1 \, , \, i_2 \in I_2 \, \dots$
However, one has to be careful when using it, because $RI + RJ \subseteq I+J$ does not mean $ri +rj \in I+J$ but $r_1 i+r_2 j \in I+J$.

 

[Math Amateur]

Thanks fresh_42 ... appreciate all your help ...

Peter