Miike012
- 1,009
- 0
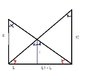
Trig work problem... (am I correct?)
If we call the height @ which the supports cross ,x, express this height as an equation in terms of H1 and H2 Only... Use similar triangle...
Are my proportion correct?
x/H1 = (L1-L)/L1
x/H2 = (L)/L1 = (L1-L)/L1
Because Where the two lines intersect you can see that the two angles are congruent (If I did it correctly)
Thus L1-L = L
And Are my congruent angles in my picture correct?
Homework Statement
If we call the height @ which the supports cross ,x, express this height as an equation in terms of H1 and H2 Only... Use similar triangle...
Are my proportion correct?
x/H1 = (L1-L)/L1
x/H2 = (L)/L1 = (L1-L)/L1
Because Where the two lines intersect you can see that the two angles are congruent (If I did it correctly)
Thus L1-L = L
And Are my congruent angles in my picture correct?