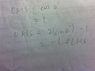- #1
davon806
- 148
- 1
Homework Statement
Please see the attached.
Q1.Why 0° is not a solution of the equation cosθ = 2sinθ - 1?
What's wrong with my steps?
Q2:http://www.wolframalpha.com/input/?i=cosx+=+2sinx+-+1
From the graph,the x-coordinate of the intersection point does NOT equal to the answer
that I calculated in the attached
(0° +360°n or 180° + 360°n or 53.1°+360°n or 126.9° + 360°n),
why?
Homework Equations
The Attempt at a Solution
see the attached.