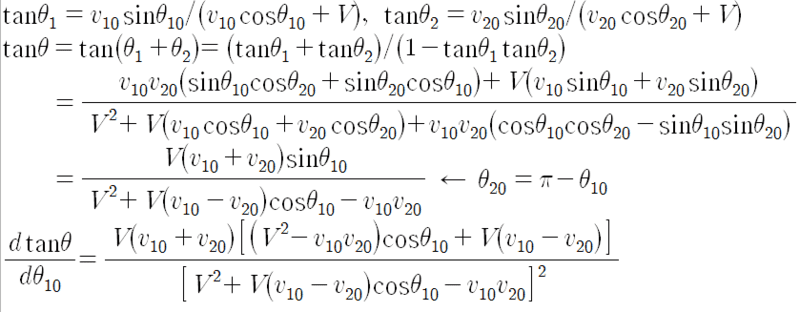emaz said:
Hi, can I ask you how you solved the problem? I got stuck just the way you did in the posts above.
I solved it! I'll copy and paste my solution, which could be useful in case someone comes across this thread.
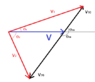
It would have been much easier if the book had given a different name to the angle ##\theta_{0}##. In fact, it is not to be intended as the same angle as the one introduced by the book in prior graphical constructions and problems. Hence, even if the problem is conceptually very simple, this might create confusion.
For the sake of completion, to bring this post to an end, I shall add some details for the solution (also to try and redeem myself from some careless mistakes :) ).
The function we have to analyze is:
$$ \begin{align}\tan{\theta} = \frac {(v_{10}+v_{20})V\sin{\theta_{0}}}{V^2+\left(v_{10}-v_{20} \right)V\cos{\theta_0 - v_{10} v_{20} }} \nonumber\end{align}$$
or equivalently:
$$ \begin{align}\cot{\theta} = \frac {V^2+\left(v_{10}-v_{20} \right)V\cos{\theta_0 - v_{10} v_{20} }}{(v_{10}+v_{20})V\sin{\theta_{0}}} \nonumber\end{align}$$ where ##\theta_{0} \in \left[0,\pi \right]##, ##V \geq 0##.
In order to find the extrema, I took the derivative with respect to ##\theta_{0}## and found the expression:
$$ \begin{align} \frac {\partial\cot{\theta}} {\partial\theta_{0}} = \frac {(-v_{10}+v_{20})V^2-V\cos\theta_{0}\left[V^2-v_{10}v_{20}\right] }{(v_{10}+v_{20})V^2\sin^2\theta_{0}} \nonumber\end{align}$$
By setting the result to 0 one gets: $$ \begin{align} \cos\theta_{0}=\frac{(v_{20}-v_{10})V}{V^2-v_{10}v_{20}} \nonumber\end{align}$$
One should notice that the formula ## \begin{align} \cos\theta_{0}=\frac{(v_{20}-v_{10})V}{V^2-v_{10}v_{20}} \nonumber\end{align} ## holds only when the cosine obviously lies in the interval ##\left[-1,1\right]##; after some calculations, one finds that this happens when ##V \geq v_{20} ~\text{or}~ V\leq v_{10}##, meaning that when ##v_{10}<V<v_{20}## the derivative of ##\cot{\theta}## does not change sign.
Moreover, one could calculate the derivative of the cotangent with respect to ##V## and find the expression:
$$ \begin{align} \frac {\partial\cot{\theta}} {\partial V} = \frac { V^2+v_{10}v_{20} } { (v_{10}+v_{20})V^2\sin\theta_{0} } \nonumber\end{align}$$
which is positive for all values of ##V##.
This is why ##\cot{\theta}## may assume all the values between ##0## and ##\pi## when ##v_{10}<V<v_{20}##, because ## \frac {\partial\cot{\theta}} {\partial\theta_{0}}\neq 0## and ## \frac {\partial\cot{\theta}} {\partial V} \neq 0## ##\forall ~V, \theta_{0}## in that interval and it is easy to see that if ##V## is kept constant and ##\theta_{0}## is varied between 0 and ##\pi##, ##\cot\theta## spans the interval ##\left]-\infty,+\infty \right[##; similarly, if ##\theta_{0}## is kept constant and ##V## is varied between 0 and +##\infty##, ##\cot \theta## spans the interval ##\left]-\infty,+\infty \right[##.
When ##V \leq v_{10}##, it is easy to see that ##\cot{\theta}## has a maximum value. In fact, ## \lim_{\theta_{0} \rightarrow 0^+} {\cot(x)} = -\infty##, ##\lim_{\theta_{0} \rightarrow \pi^-} {\cot(x)} = -\infty## and the maximum value of the cotangent is reached when:
$$ \begin{align} \cos\theta_{0}=\frac{(v_{20}-v_{10})V}{V^2-v_{10}v_{20}} \nonumber\end{align}$$
The calculation of the maximum value leads to:
$$ \begin{align} \cot{\theta} &= \frac {V^2+\left(v_{10}-v_{20} \right)V\cos{\theta_0 - v_{10} v_{20} }}{(v_{10}+v_{20})V\sin{\theta_{0}}}= \nonumber \\
\dots &= \frac{v_{20}-v_{10}}{v_{20}+v_{10}} \frac{ \sin{\theta_{0}} }{\cos{\theta_{0}}}= \dots \nonumber \\
&=-\frac{\sqrt{\left( V^2-v_{10}v_{20}\right)^2-\left(v_{20}-v_{10}\right)^2 V^2}}{\left( v_{10}+v_{20}\right)V } \nonumber \end{align}$$
Then, after transforming the cotangent into a sine, one gets:$$ \begin{align} \sin\theta=\frac{(v_{20}+v_{10})V}{V^2+v_{10}v_{20}} \nonumber\end{align}$$ If we put: $$ \begin{align} \alpha=\sin^{-1}{\left(\frac{(v_{20}+v_{10})V}{V^2+v_{10}v_{20}}\right)} \nonumber\end{align}$$
then, in the interval where ##V\leq v_{10}##, we have the following ranges for ##\theta##: ##\pi-\alpha \leq \theta \leq \pi##.
Similarly, when ##V \geq v_{20}##, it is easy to see that ##\cot{\theta}## has a minimum value. In fact, ## \lim_{\theta_{0} \rightarrow 0^+} {\cot(x)} = +\infty##, ##\lim_{\theta_{0} \rightarrow \pi^-} {\cot(x)} = +\infty## and the minimum value of the cotangent is reached when ##\theta=\alpha##. In this case the ranges for ##\theta## are: ##0 \leq \theta \leq \alpha## (the equality ##\theta=0## is satisfied only when ##V \rightarrow +\infty##).
To summarize:
$$ \begin{align} &\text{if}~~ v_{10}<V<v_{20} \rightarrow 0<\theta<\pi \nonumber \\
\nonumber \\
&\text{if}~~ V\leq v_{10} \rightarrow \pi-\alpha \leq \theta \leq \pi \nonumber \\
\nonumber \\
&\text{if}~~ V\geq v_{20} \rightarrow 0\leq\theta\leq\alpha \nonumber\end{align} $$
where $$ \begin{align} \alpha=\sin^{-1}{\left(\frac{(v_{20}+v_{10})V}{V^2+v_{10}v_{20}}\right)} \nonumber\end{align}$$