gex
- 36
- 2
Mentor note: Thread moved from technical section, so missing the homework template.
Hi all, I have a homework problem which asks me to compute the complex number cos(π/4 + π/4 i).
I've been playing around with it for a while now and just can't seem to get the answer I get when using Wolfram Alpha to verify. Attached is my most recent attempt at solving the problem, I'd love some input as to where I'm going wrong. Thank you in advance.
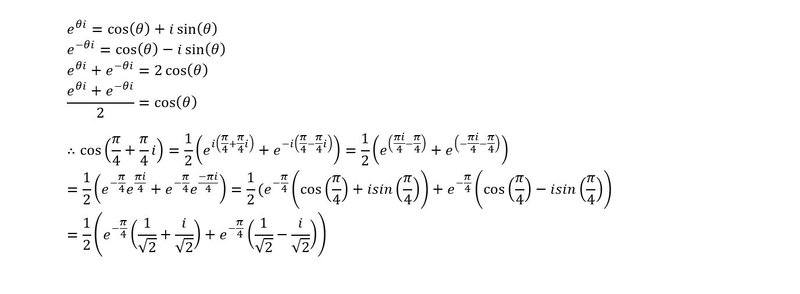
Hi all, I have a homework problem which asks me to compute the complex number cos(π/4 + π/4 i).
I've been playing around with it for a while now and just can't seem to get the answer I get when using Wolfram Alpha to verify. Attached is my most recent attempt at solving the problem, I'd love some input as to where I'm going wrong. Thank you in advance.
Attachments
Last edited by a moderator: