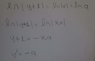Trouble with needless of absolute value

[mech-eng]

Hi, while solving differential equations problems we have to sometimes use absolute value while
taking an integral of which 1 over a function. But in some problems I understand that we do not
have to use absolute value sign for example if the function related with atom number which can
never be a negative number we do not have to use absolute value. But in the picture I added here there is no sign about physical meaning of the problem so I think we should use absolute value and so there should have to be two different answers. The second picture of handwritting is
my other solution. The last one is a topic related with the problems. Have a nice day.

 

[HallsofIvy]

Equation 2.8 certainly should be $ln|y+ 1|= ln|x|+ cnst= ln|x|+ ln|a|= ln|ax|$

However, once we have gotten rid of the logarithms on both sides, we have y+ 1= ax, whether y, x, and a are positive or negative, and no longer need the absolute value signs.

 

[mech-eng]

Equation 2.8 certainly should be $ln|y+ 1|= ln|x|+ cnst= ln|x|+ ln|a|= ln|ax|$

However, once we have gotten rid of the logarithms on both sides, we have y+ 1= ax, whether y, x, and a are positive or negative, and no longer need the absolute value signs.

But in this situation y +1 might be positive whereas ax might negative so y + 1 might equal to -ax which leads to two different equalities, isn't it?

 

[HallsofIvy]

No, that can't happen. "a" is a constant determined by the initial value. If we are given an initial value $(x_0, y_0)$ such that $y_0+ 1$ and $x_0$ have the same sign, then a will be positive and y+ 1 and x will have the same sign for all x. If we are given an initial value $(x_0, y_0)$ such that $y_0+ 1$ and $x_0$ have opposite sign, then a is negative and y+1 and x will have opposite sign for all x. In either case, y+ 1 and ax will have the same sign