carlcla
- 11
- 6
- Homework Statement
- Calculate the trusses in each beam of one of the cross sections
- Relevant Equations
- N/A
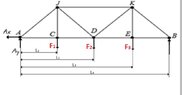
I need to calculate the forces in each of the beams in one of the two equal cross sections of the truss attatched in the picture. The second picture is the cross section of the truss.
As you can see on the 3d picture of the truss the loads are attatched with equal distance inbetween the 2 "cross sections" that make up the truss. When calculating forces in one of the cross sections as in the 2. Picture, do i also need to devide the loads in half as I am only calculating for half the truss?
As you can see on the 3d picture of the truss the loads are attatched with equal distance inbetween the 2 "cross sections" that make up the truss. When calculating forces in one of the cross sections as in the 2. Picture, do i also need to devide the loads in half as I am only calculating for half the truss?