Trying to understand the basics of Hooke's law

[archaic]

Hello, I need some help on understanding what this book is trying to convey.

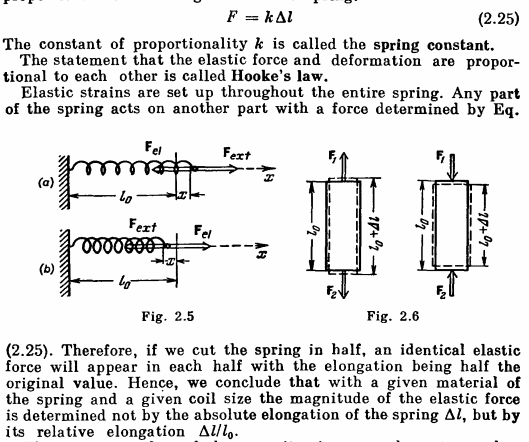
How does "any part of the spring acts on another part"? Doesn't (2.25) just give us the "operator force" and, since the spring is at equilibrium, the elastic force? What exactly is strain?
And I am failing to see the "therefore" part and the "Hence" after it, I haven't understood what is before so .. How is it the elastic force that will appear equal to the initial one?
Thank you for your time!

 

[jedishrfu]

You would model the spring as smaller connected springs or box elements with some force between them like ganging up magnets to make a stronger magnet.

So imagine a spring of 10cm and you stretch it to 20cm and need to use X Newtons to do it.

if you then cut the spring in half ie 5cm segments then you'll need half the force to pull a segment 5cm ie stretching it from 5cm to 10cm.

I got this part wrong. Thanks go to @Chestermiller for pointing it out and for Wikipedia to explain it better.

Springs in series ie two 5cm springs would have a different spring constant computed from the original to be

$k_{halfspring} = 2 * k_{fullspring}$

https://en.m.wikipedia.org/wiki/Series_and_parallel_springs
NOTE: Hooke's law is only valid in some cases, not all springs obey the law but those that do make your life easier.

 

[GreatestPhysician99]

Hooke's law just says that any spring resists to the change of its original width by exerting a force on the object making the change . The more we displace the spring , the more the spring resists to the displation

 

[256bits]

And I am failing to see the "therefore" part and the "Hence" after it, I haven't understood what is before so .. How is it the elastic force that will appear equal to the initial one?

I can see why.
The book has a confusing way to describe a spring.

Since the spring is in equilibrium, there is no acceleration of the spring, and the forces at both ends are equal.
Also, it follows that at any point within the spring, the opposing forces are also equal on either section on either side of that point.
so we could cut the spring in half and the new each half length spring would have the same forces on the ends as before, but with half the total elongation.

Strain, for a spring, is just the amount of deflection ( elongation ) per length.
For the whole spring that would be ( final length - initial length ) / initial length. ( the Δl / L ).

 

[archaic]

I posted this question but expressed it more thoroughly on physics.stackexchange, I'll share the answer

 

[hutchphd]

if you then cut the spring in half ie 5cm segments then you'll need half the force to pull a segment 5cm ie stretching it from 5cm to 10cm.

This is not correct, unless I misunderstand. If you cut a spring in half, the spring constant doubles.

 

[Chestermiller]

What the article is saying is that the more correct form of the equation should be $$F=K\frac{\Delta l}{l_o}$$where $l_o$ is the original length and K is a constant (with units of force) that is independent of the original length of the spring. In this equation, the axial strain of the spring is $$\epsilon=\frac{\Delta l}{l_0}$$So, in terms of the usual spring constant, $$k=\frac{K}{l_o}$$This means that the usual spring constant is inversely proportional to the unstretched length of the spring. So if the spring is half as long, its spring constant is twice as large. So, if you have a spring 10 cm long, and you stretch it to 20 centimeters, each half of the spring stretches from 5 cm to 10 cm, and, of course, has the same force as the overall spring.

 

[jedishrfu]

I found this writeup on springs and Hooke's law that provides a pretty description of the spring cutting problem and why the k constant changes:

https://www.futurelearn.com/courses/maths-power-laws/0/steps/12143

Suppose we have a given spring with a given spring constant k. What happens if we cut this spring into two equally sized pieces? One of these shorter springs will have a new spring constant, which will be 2k. More generally, the spring constant of a spring is inversely proportional to the length of the spring, assuming we are talking about a spring of a particular material and thickness.

So suppose we cut the spring in the example above exactly in two, creating two shorter springs each of length 33 cm. One of the smaller springs will have a spring constant which is twice the original. That is because the spring constant and the length of the spring are inversely proportional. That means that the original mass of 3030 gm will only yield a stretch of 11 mm on the shorter spring. The larger the spring constant, the smaller the extension that a given force creates.

...