- #1
phsopher
- 180
- 4
I'm trying to understand why the WKB approximation doesn't seem to work in the following case.
Suppose you have a particle of mass ##m## in a potential ##V(x)=q m\cos(2mx/\hbar)##, where ##q\ll 1##. Consider then the stationary solution with energy ##E=m/2##. The Schroedinger equation is then
[tex]\psi'' + (1-2q\cos 2z)\psi = 0 \qquad (1)[/tex]
where I defined a dimensionless variable ##z=mx/\hbar##. With the ansatz ##\psi(z) = A(z)e^{iS(z)}## this reduces to
[tex]W^2\left[1-\frac{3}{4}\left(\frac{W'}{W^2}\right)^2 + \frac{1}{2}\frac{W''}{W^3}\right] = 1-2q\cos 2z \equiv \omega^2(z) [/tex]
where I have also used the conservation of the Wronskian (current) which gives ##(S'/W)'=0##.
Now, if the latter two terms in the square brackets are small then I should be able to solve this iteratively with the leading solution simply being ##W=\omega## so the solution is
[tex]\psi = \frac{1}{\sqrt{2\omega}}e^{i\int\omega\mathrm dz}[/tex]
This is the gist of the WKB approximation as I understand it. In this case indeed ##\omega'/\omega^2, \omega''/\omega^3 \ll 1## so I don't see why this wouldn't work. However, this produces an oscillating solution with a constant amplitude. In reality, Equation (1) is the Mathieu equation and the amplitude of the oscillations is known to be amplified exponentially (parametric resonance).
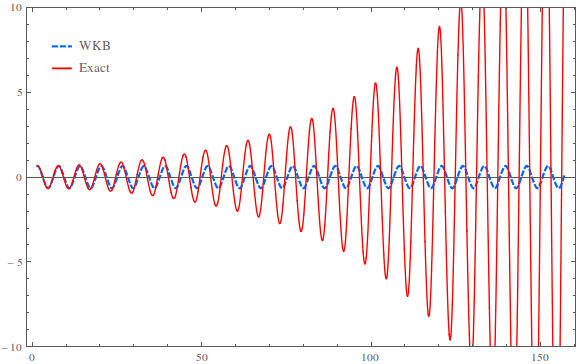
I don't quite get why the WKB approximation fails here. Below is a numerical comparison between second order WKB solution and the exact numerical solution of (1).
Suppose you have a particle of mass ##m## in a potential ##V(x)=q m\cos(2mx/\hbar)##, where ##q\ll 1##. Consider then the stationary solution with energy ##E=m/2##. The Schroedinger equation is then
[tex]\psi'' + (1-2q\cos 2z)\psi = 0 \qquad (1)[/tex]
where I defined a dimensionless variable ##z=mx/\hbar##. With the ansatz ##\psi(z) = A(z)e^{iS(z)}## this reduces to
[tex]W^2\left[1-\frac{3}{4}\left(\frac{W'}{W^2}\right)^2 + \frac{1}{2}\frac{W''}{W^3}\right] = 1-2q\cos 2z \equiv \omega^2(z) [/tex]
where I have also used the conservation of the Wronskian (current) which gives ##(S'/W)'=0##.
Now, if the latter two terms in the square brackets are small then I should be able to solve this iteratively with the leading solution simply being ##W=\omega## so the solution is
[tex]\psi = \frac{1}{\sqrt{2\omega}}e^{i\int\omega\mathrm dz}[/tex]
This is the gist of the WKB approximation as I understand it. In this case indeed ##\omega'/\omega^2, \omega''/\omega^3 \ll 1## so I don't see why this wouldn't work. However, this produces an oscillating solution with a constant amplitude. In reality, Equation (1) is the Mathieu equation and the amplitude of the oscillations is known to be amplified exponentially (parametric resonance).
I don't quite get why the WKB approximation fails here. Below is a numerical comparison between second order WKB solution and the exact numerical solution of (1).
Last edited: