B How Does the Twin Paradox Affect Aging?

[Daniepie]

I'm just trying to develop a general understanding of the 'twin paradox', so my description of this is will be a bit poor.
I feel like I have a sound understanding so far on the topic, but the only thing that I can't seem to find an answer for is this scenario;
Say you have the classic twin paradox situation, what I don't understand is what causes the body to 'slow down' its aging process. So I understand that to the twin on the ground say 30 years pass, but their twin traveling returns to be 2 years older.
But why is it that to the traveler it only felt like two years and so they only aged two years? What is actually happening to the body during this time?

 

[BvU]

Hello Dan,

The traveling twin experiences acceleration, the grounded one does not.

 

[Ibix]

The simplest answer is that the elapsed time you experience turns out to be the "length" (called the "interval") of the path you follow through spacetime. Having different elapsed times for two people who followed different routes through spacetime isn't much different from the familiar fact that two people who follow different routes through space may travel different distances. So nothing causes one person to age slowly. They just took a shortcut.

That time acts like a distance may seem hard to swallow, but it's a consequence of time and space being parts of the same thing, spacetime. Time is different from the three spatial directions in some important ways (for example, in spacetime a straight line between two events is the longest route, not the shortest, which is why the stay-at-home ends up older), but there are a lot of similarities.

I strongly recommend that you learn to draw Minkowski diagrams. They are very straightforward (just position-versus-time graphs), but they are the best tool for understanding special relativity. Far more so than studying paradoxes.

 

[Ibix]

The traveling twin experiences acceleration, the grounded one does not.

While true, this doesn't explain the aging difference. It's possible to construct variants on the twin paradox where both twins undergo accelerations and ones where no-one accelerates yet the twins age differently.

 

[phinds]

...what causes the body to 'slow down' its aging process

Nothing causes it because it doesn't happen. You are confusing differential aging with time dilation. It's as though you drive a car from New York to Boston and it takes you a day and you have a friend who makes the same trip except he goes by way of Chicago and it takes him 4 days. Did either of your body rates change during the trips?

 

[itfitmewelltoo]

While true, this doesn't explain the aging difference. It's possible to construct variants on the twin paradox where both twins undergo accelerations and ones where no-one accelerates yet the twins age differently.

Are you referring to Special or General when you say "it's possible...". As I understand it, the "paradox" is entirely restricted to Special Relativity and is a consequence of the lack of accounting for acceleration and gravity. The paradox is resolved in GR. It is the acceleration that accounts for time dilation and length contraction.

 

[Ibix]

Are you referring to Special or General when you say "it's possible...". As I understand it, the "paradox" is entirely restricted to Special Relativity and is a consequence of the lack of accounting for acceleration and gravity. The paradox is resolved in GR. It is the acceleration that accounts for time dilation and length contraction.

It's not a paradox in SR either. GR is not required unless you want to swing round a black hole to do the turn around. It's only a paradox in common misunderstandings of relativity.

It is true that you can't construct a frame of reference for the traveling twin using only inertial coordinates. Some older sources may insist that non-inertial frames are outside the scope of SR, but that's not the modern meaning of the term. And the paradox can be resolved without reference to the traveling twin's reference frame anyway.

 

[phinds]

Are you referring to Special or General when you say "it's possible...". As I understand it, the "paradox" is entirely restricted to Special Relativity and is a consequence of the lack of accounting for acceleration and gravity. The paradox is resolved in GR. It is the acceleration that accounts for time dilation and length contraction.

No, the paradox is completely explained in SR. There's no need to bring GR into play. Gravity has nothing to do with it. Acceleration does NOT account for the time dilation or length contraction. You get both without acceleration. The acceleration explains the lack to symmetry in their paths through space-time which is what results in differential aging.

EDIT: I see ibex beat me to it

 

[Nugatory]

"The acceleration explains the lack to symmetry in their paths through space-time"

Okay, like I said, it's the acceleration that is accounted for in GR and not in SR.

In fact, SR handles acceleration just fine - google for "Rindler coordinates" for an example.

However, your misunderstanding is very common. Intro courses in SR usually don't cover problems involving acceleration because the math is appreciably more complicated, so these problems are left for more advanced classes. This leaves students with the impression that it can't be done, when actually they just haven't seen it done.

The paradox is that by SR, each must "see" the other as length contracted and time dialated. But the can't both be. SR does not resolve it.

That is indeed the paradox, but it is properly and completely explained by SR. A pretty good summary of how do this can be found online here and Taylor and Wheeler's "Spacetime Physics" is a good modern textbook that covers this topic with more sophistication. And for that matter...

Have you read the 1913 paper "On the Electeodynamics of moving bodies"? If so, then you can point out the section that resolves the paradox.

1905, not 1913, and the paradox is explained and resolved in the last few paragraphs of section 2.4: https://en.wikisource.org/wiki/On_the_Electrodynamics_of_Moving_Bodies_(1920_edition)

(This link is dated 1920, but that's the date of the English-language translation from the 1905 German original)

 

[Janus]

I'm just trying to develop a general understanding of the 'twin paradox', so my description of this is will be a bit poor.
I feel like I have a sound understanding so far on the topic, but the only thing that I can't seem to find an answer for is this scenario;
Say you have the classic twin paradox situation, what I don't understand is what causes the body to 'slow down' its aging process. So I understand that to the twin on the ground say 30 years pass, but their twin traveling returns to be 2 years older.
But why is it that to the traveler it only felt like two years and so they only aged two years? What is actually happening to the body during this time?

This is a common question. The problem come from thinking about Relativity in terms of something that "causes" clocks to slow down. It is more about the very natures of "time" and "space" and how we measure them.
To explain what I mean, I'll use an analogy. Imagine time and space like a map. North and South is time and East and West are space. If you take two points on that map, they will have a set North-South and East-West relationship to each other. I can turn the map in any direction I like and this relationship doesn't change, as it is tied to the map itself.

This is how time and space were thought of prior to Relativity. What Relativity changes is the relationship time and space has to the map. Now instead of being tied to the map, it is tied to the Observer. Space is measured by the Observer's Left-Right and time by the Observer's Up-down. Now if I turn the map with those two points on it, their Up-down and Left-right relationships change. I can turn the map until the one point is right above the other, or so that neither point is above the other. The same thing happens leave the map where it is and rotate myself instead. My sense of Left-Right and Up-Down turns with me.

So let's consider how that works when dealing with the Twin paradox. This time we are going to use a really big map and put our observers on it. We'll leave Left-right as being space, but now front-back for each observer is time.
We'll have two observers (A and B) and start them off at the same pace from the same point.
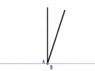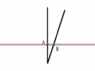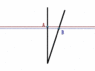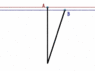
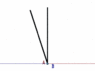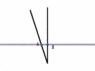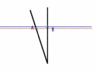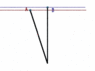
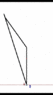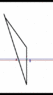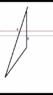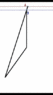
Here's how things appear to A.

The red line represents progress in the direction he is walking (which in this analogy represents progress in time). As you can see, By A's reckoning, he progresses through time faster than B. (he ages faster)

If we switch to B's perspective we get this:

According to him, he is the one that makes better progress through time and thus ages the faster of the two.

Unless something changes, this will remain the case. In the Twin paradox, something does change, one of the twin changes his velocity and heads back toward the other twin. In our analogy, this is the equivalent of one of our observer's changing direction and walking back towards the path of the other observer. We'll choose B for our analogy.
Thus from A's perspective, we see this.

Even after B makes his turn he continues to make less progress in time an age slower than A does. When he crosses A's path, he is directly "behind" A in time but in the same spot in space (measured left and right). Thus in the twin paradox, according to A, B ages more slowing than he does during the whole trip and when they reunite has aged less.

What happens according to B?

If we just take our first view for B and extend it we get this
.

B, after changing direction starts to make slower progress than A. A catches and passes B, and B ends up being behind A. A still ends up aging more than B.

But this isn't exactly what happens according to B, But rather what would happen according to some one who continued in B's original direction after B changed directions.

For what happens according to B, we have to consider what I said above about what happens if we turn the map or turn relative to the map. When B changes direction, so does his relationship relative to A does in terms of time.

What happens is this:

B starts out heading "straight up". After he changes direction he still is heading "straight up" (by his perception he is still walking "forward", so the whole "map" has to rotate. But when this happens, A goes suddenly from being "behind" B to being "ahead" of B. B then starts to catch up, but never does before A crosses its path.

So even though at no time does A or B change the pace at which they walk, B ends up "behind" A
B took a different path in space-time, and as a result, spent less time by his clock doing so than A did.

The important thing to keep in mind is that in these animations the Up and Down directions are measurements of personal time, and the left and right directions are space(limited to one dimension in space.)

 

[Herman Trivilino]

I feel like I have a sound understanding so far on the topic, but the only thing that I can't seem to find an answer for is this scenario; Say you have the classic te..

The aging process does not slow down. That is the flaw in your logic. The aging process follows the proper time of the twin who's doing the aging. One ages two years for every two years of proper time, the other ages 30 years for every 30 years of proper time.

A remaining question is why the twins find, upon their reunion, that different amounts of proper time have elapsed.

The easiest answer I know is that they take different paths through spacetime.

 

[Daniepie]

Thank you so much for all your responses!
I see that I lacked a lot more understanding of it than I thought and my view was fixated on the non-existent "3rd party preferred observer with an over-riding definition of what normal is for some preferred frame." as Grinkle mentioned.
I've encompassed all of the ideas that related onto a piece of paper with the diagrams given; literally grateful for all of the diagrams and explanations because they were a great help!
Now is my time to further sus out spacetime, GR, and SR

 

[Janus]

An attempt at your “show the math” request. This is the same problem worked out in the Scientific American thread, with a different gamma.

One twin, A, stays on Earth. The other twin, B, accelerates at a very, very tiny rate (so that acceleration is irrelevant) until he reaches 0.7c. Note: we can accelerate as slowly as we want so, again, reaching the initial speed is irrelevant.

Twin B will travel to a planet that is 7 light years away according to measurements taken at rest with respect to Earth (i.e. this is the distance A measures).

Due to length contraction, as Twin B travels, to him the distance appears to be 5 light years. Thus, traveling at 0.7c, Twin B gets there in 5/.7 = 7.14 years (approximately).

Meanwhile, Twin A sees Twin B reach the planet in (7/.7 + 7) years = 17 years (7/.7 for the actual travel time of Twin B and 7 more years for light to reach Twin A after Twin B arrives). Thus, to Twin A, Twin B’s clock appesrs to be running 7.14/17 = 42% the normal rate.

Both get different times, but both see the other as ticking at the same slowed rate.Now look what happens on the way back. Since according to Earth the total distance is 14 light years, and since the spaceship traveled at 0.7c, the total trip must take 20 years. But 17 were spent on the way there according to Twin A. Thus, according to Twin A, the remaining trip must take 3 years. Thus, on the way back Twin A sees Twin B’s clock tick 7.14 years in only 3 year’s time. So now Twin B’s clock is ticking 2.38 times faster for 3 years.

Meanwhile, Twin B has a total trip time of 14.28 years, and 7.14 years remaining. But by the time Twin B gets to the planet, according to Twin B, 3 years have passed for Twin A. Since the total trip according to Twin A must be 20 years, Twin B must see 17 years tick on Twin A’s clock while only 7.14 tics on his own clock. Thus, Twin B sees Twin A’s clock tick at 17/7.14 = 2.38 times the rate of his own clock, this time for 17 years.

Thus you see the symmetry and asymmetry for each twin. The “moving” twin sees the other twin’s clock tick faster for longer. By the time the reunite, Twin B will be younger than Twin A.

No dependence upon acceleration other than to turn Twin B around so he returns home.
That’s my take on it, anyway. I’m sure someone else has something better.

It appears that you are using the Doppler shift explanation here. But it is a bit muddled. For example, when you say

When Twin B reaches the planet, he sees Twin A’s clock as it was 7 years ago, which means 10-7 = 3 years have passed for Twin A according to Twin B. So according to Twin B, Twin A’s clock is 3/7.14 = 42% the rate of Twin B’s clock.

You are talking about what B sees, but you are working in the frame of A. In B's frame, he doesn't see A as it was 7 years ago, but as it was 3 years ago by his clock. (according to B, that's how far apart A and B was when the light left A) You also say, that that 3 years have passed for A according to B. But three years is the reading on Clock A that Clock B visually sees at that moment, and not the actual time on Clock A according to B at that moment (which is 5 years).

You also claim that acceleration is not important to this scenario, but it is. As A watches B recede, he sees B's clock run slow until he sees B do his turn around and then he sees B clock run fast. But there is a 7 year lag between B actually turning around and B turning around, Thus he sees B's clock run slow for 17 years and fast for 3 years. B however sees A's clock run slow for 7.14 years and fast for 7.14 years. This is because he sees an instant shift in the Doppler shift from A when he turns around. In other words, because he was the one that underwent an acceleration, he sees that instant change in Doppler shift, while A, who doesn't accelerate, has to wait to see the effects of B changing velocity.

 

[Justin Hunt]

Why can’t both twins see the other one as speeding away and then coming back? I get how if two objects are in motion relative to each other the perspective that you are stationary and the other is moving is equally valid for both. But, Why doesn’t this hold for acceleration?

 

[PeroK]

Why can’t both twins see the other one as speeding away and then coming back? I get how if two objects are in motion relative to each other the perspective that you are stationary and the other is moving is equally valid for both. But, Why doesn’t this hold for acceleration?

Because you can feel and measure a definite value for acceleration.

 

[Arkalius]

Why can’t both twins see the other one as speeding away and then coming back? I get how if two objects are in motion relative to each other the perspective that you are stationary and the other is moving is equally valid for both. But, Why doesn’t this hold for acceleration?

Because acceleration can be measured within a given reference frame without having to consider anything in motion relative to your frame. An accelerometer on the ship will tell you if its accelerating or not. Furthermore, a third, inertial observer will note the accelerating ship change its motion while the non-accelerating ship remains in constant relative motion.

 

[PeroK]

... this also ties in with why Newton's second law of motion is $F = ma$.

Force and acceleration are measurable and invariant across all inertial reference frames. Velocity, on the other hand, is frame dependent: Different inertial observers measure a different velocity. So you cannot assign an absolute value to your velocity.

 

[robphy]

Force and acceleration are measurable and invariant across all inertial reference frames. Velocity, on the other hand, is frame dependent: Different inertial observers measure a different velocity. So you cannot assign an absolute value to your velocity.

Note that the "magnitude of relative-velocity [between two given inertial observers]" is frame-independent.

 

[PeroK]

Note that the "magnitude of relative-velocity [between two given inertial observers]" is frame-independent.

Can you give an example? I'm not sure what that means.

 

[jbriggs444]

Note that the "magnitude of relative-velocity [between two given inertial observers]" is frame-independent.

Pedant point:

That is almost a tautology. The velocity of the first observer relative to the second's rest frame is what it is. Everyone agrees on that value because the frame from which the measurement is to be taken is specified. Nobody else's frame enters in.

The one tidbit of real information is that the velocity of the second observer relative to the first's rest frame is equal and opposite. But that's already captured in the fact that one can even say "relative velocity between two inertial observers". If the two relative velocities could be different than that phrase could not properly be used.

Edit: If by "relative velocity" one means "closing velocity according to a third-party frame" then that is not a relativistic invariant.

 

[robphy]

The geometric analogy is that the angular measure of a line is not invariant under rotations, but the angle measure between two lines is.
I guess I didn't finish writing out the thought.
I don't think that lack-of-invariance of velocity argument is strong enough.
The argument must focus on the fact that the traveler is non-inertial [as PeroK and others did earlier].

 

[Sorcerer]

It appears that you are using the Doppler shift explanation here. But it is a bit muddled. For example, when you say
You are talking about what B sees, but you are working in the frame of A. In B's frame, he doesn't see A as it was 7 years ago, but as it was 3 years ago by his clock. (according to B, that's how far apart A and B was when the light left A) You also say, that that 3 years have passed for A according to B. But three years is the reading on Clock A that Clock B visually sees at that moment, and not the actual time on Clock A according to B at that moment (which is 5 years).

You also claim that acceleration is not important to this scenario, but it is. As A watches B recede, he sees B's clock run slow until he sees B do his turn around and then he sees B clock run fast. But there is a 7 year lag between B actually turning around and B turning around, Thus he sees B's clock run slow for 17 years and fast for 3 years. B however sees A's clock run slow for 7.14 years and fast for 7.14 years. This is because he sees an instant shift in the Doppler shift from A when he turns around. In other words, because he was the one that underwent an acceleration, he sees that instant change in Doppler shift, while A, who doesn't accelerate, has to wait to see the effects of B changing velocity.

What I meant by acceleration isn’t important is that it is only the cause of the asymmetry, but it the asymmetry that ultimately causes the difference. Is that a fair statement?

 

[phinds]

What I meant by acceleration isn’t important is that it is only the cause of the asymmetry, but it the asymmetry that ultimately causes the difference. Is that a fair statement?

Yes. Post #6 in this thread:
https://www.physicsforums.com/threads/scientific-american-on-the-twin-paradox.940379/#post-5945938
discusses a scenario without acceleration (but, of necessity, WITH the asymmetry)

 

[SiennaTheGr8]

I think David Morin does a nice job covering the relativity of simultaneity. In particular, I like that he names the "rear clock ahead" phenomenon (see p. 11 of this PDF).

Here's a seemingly bizarre consequence of the "rear clock ahead" effect that Don Koks points out:

Two chapters back, in (5.11), we saw that when two clocks synchronised in their shared rest frame move past us with constant velocity v, the spatially trailing clock leads its partner by a time vL₀/c², where their proper separation is L₀.

But on some reflection this leads to a difficulty. Suppose that one of the synchronised clocks sits by our side, while the other lies in a distant galaxy, one thousand million light-years away. Leaving aside questions as to the meaning of distance on a cosmological scale, set their proper separation to be L₀ = 10⁹ light-years. Now suppose that we on Earth pace slowly to and fro, moving with speed v = 10⁻⁹c in each direction.

In that case, the clock next to us alternately leads and trails its partner by one year. But because it’s right next to us, we can see that its time is not changing at all by any more than the few seconds we spend pacing. That implies that the clock in the distant galaxy is alternately jumping ahead of us by one year and then suddenly dropping behind by the same amount; and this see-sawing continues for as long as we pace to and fro. Can this apparently nonsensical state of affairs really be happening?

Yes, the time we measure on the distant clock really is swinging back and forth wildly, as we accelerate periodically to switch our walking direction. This is a symptom of the fact that as we pace to and fro, we no longer inhabit a single inertial frame; in fact, we no longer inhabit even a single accelerated frame.

Source: https://books.google.com/books?id=ytTFazXPy6oC&pg=PA233

That's what happens in the twin paradox when the rocket-twin changes directions: Earth-twin's clock switches from being the "front clock" to the "rear clock" (in relation to a synchronized clock at the turnaround point). For the rocket-twin, it's like the Earth-twin has suddenly "jumped ahead" very far into the future, but really it's the rocket-twin who's made a sudden change.

 

[JulianM]

I think David Morin does a nice job covering the relativity of simultaneity. In particular, I like that he names the "rear clock ahead" phenomenon (see p. 11 of this PDF).

Here's a seemingly bizarre consequence of the "rear clock ahead" effect that Don Koks points out:
Source: https://books.google.com/books?id=ytTFazXPy6oC&pg=PA233

That's what happens in the twin paradox when the rocket-twin changes directions: Earth-twin's clock switches from being the "front clock" to the "rear clock" (in relation to a synchronized clock at the turnaround point). For the rocket-twin, it's like the Earth-twin has suddenly "jumped ahead" very far into the future, but really it's the rocket-twin who's made a sudden change.

Why would the clock run slower when it is moving away and faster when it is coming back?
If it does what happens to a long object as it passes the return point and it has one clock running fast and the other more slowly as it passes?

 

[phinds]

Why would the clock run slower when it is moving away and faster when it is coming back?

There is no actual change in the behavior of the clock itself, we're talking about how it LOOKS to the observers.

 

[Herman Trivilino]

Here's a seemingly bizarre consequence of the "rear clock ahead" effect that Don Koks points out:

Yes, the time we measure on the distant clock really is swinging back and forth wildly, as we accelerate periodically to switch our walking direction.

Does this claim of "wild" play on an emotion? This wild swinging is nothing but a notion of simultaneity swinging, there's nothing physical in that, so in that sense it's not wild.

 

[JulianM]

There is no actual change in the behavior of the clock itself, we're talking about how it LOOKS to the observers.

When you say LOOKS do you mean it's not real?

 

[phinds]

When you say LOOKS do you mean it's not real?

It's completely real to the looker, it's just not real in the frame of reference of the clocks.

 

[bhobba]

Why can’t both twins see the other one as speeding away and then coming back? I get how if two objects are in motion relative to each other the perspective that you are stationary and the other is moving is equally valid for both. But, Why doesn’t this hold for acceleration?

SR deals with inertial frames. Inertial frames are, by definition homogeneous and isotropic in space, and homogeneous in time, meaning all points, directions and times are equivalent. One twin remains in an inertial frame. Another twin accelerates - breaking the defining conditions of an inertial frame - during accelerations particles will all by themselves move in some direction - directions are no longer equivalent. Now how does SR handle that - simple - it considers the non-inertial system as consisting of a large number of inertial systems of very short duration (the typical intuitive calculus thing often used in physics) - in those systems, for a very short period of time SR holds and the analysis proceeds that way. Its done by what is called world lines - you can look up the technicalities eg:
http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_spacetime.html

That it, that's all.

Now regarding a mechanical explanation/basis of SR - we have one - it's called LET. It's a backwater these days but some people have worked on it - I seem to recall John Bell, of Bells Theorem fame, was one, but don't hold me to it. However the question itself is quite deep and requires a thread of its own. But just a short comment here - Poincare asked Einstein what is the mechanical basis of SR in 1911 - Einstein replied - none - to which Poincare - yes the great Poincare - stood there in shock. He knew it was a penetrating question that Einstein simply dismissed. We now know its even more penetrating than could have been known at the time - but that requires its own thread.

Thanks
Bill

 

[Ibix]

When you say LOOKS do you mean it's not real?

What do you mean by "real"? The problem is that everything you know about the universe is a matter of interpretation, and what relativity forces on you is an interpretation that's a bit different from your intuitive model.

For example, you are walking towards the town hall and I'm walking away. As we pass, I glance over my shoulder at the clock, which you can see anyway. We agree that it reads exactly noon. We must agree, because we are in the same place looking at light that reflected off the clock and reached us at the same moment, and we can easily set up paradoxes if we disagree (for example, we agree beforehand that if we pass before noon, I shove you over; if we pass after noon you shove me over; if we pass on the dot of noon we just walk on - we must agree on the time or we end up doing different things).

But we know that the speed of light is finite, so we're actually seeing the clock as it was a few hundred nanoseconds ago. What time is it, now? All we have to do is work out how far away the clock was when it emitted the light we're seeing now and correct for that. The problem is, we don't agree how far away the clock was. According to you, you are stationary and the clock is coming towards you, so it was a tiny bit further away then than it is now. According to me, the clock is moving away from me, so it was a tiny bit closer then than it is now. But we agree the reading we can see. What's going on?

There are two possible solutions. One is that light has a variable speed, so it's traveling a bit slower according to me than according to you. That's what was expected prior to Einstein; Michelson and Morley's experiment was trying to detect this kind of variation. The other is that the speed of light is constant in all frames, but we don't agree on what "at the same time" means, nor on what rate the clock is ticking at. That's relativity.

So, to get back to your original question "is it real", the answer is that pretty much everything is a matter of interpretation. It's just as real an effect as everything else - but other people's different interpretations are just as legitimate.

 

[JulianM]

What do you mean by "real"? The problem is that everything you know about the universe is a matter of interpretation, and what relativity forces on you is an interpretation that's a bit different from your intuitive model.

For example, you are walking towards the town hall and I'm walking away. As we pass, I glance over my shoulder at the clock, which you can see anyway. We agree that it reads exactly noon. We must agree, because we are in the same place looking at light that reflected off the clock and reached us at the same moment, and we can easily set up paradoxes if we disagree (for example, we agree beforehand that if we pass before noon, I shove you over; if we pass after noon you shove me over; if we pass on the dot of noon we just walk on - we must agree on the time or we end up doing different things).

But we know that the speed of light is finite, so we're actually seeing the clock as it was a few hundred nanoseconds ago. What time is it, now? All we have to do is work out how far away the clock was when it emitted the light we're seeing now and correct for that. The problem is, we don't agree how far away the clock was. According to you, you are stationary and the clock is coming towards you, so it was a tiny bit further away then than it is now. According to me, the clock is moving away from me, so it was a tiny bit closer then than it is now. But we agree the reading we can see. What's going on?

There are two possible solutions. One is that light has a variable speed, so it's traveling a bit slower according to me than according to you. That's what was expected prior to Einstein; Michelson and Morley's experiment was trying to detect this kind of variation. The other is that the speed of light is constant in all frames, but we don't agree on what "at the same time" means, nor on what rate the clock is ticking at. That's relativity.

So, to get back to your original question "is it real", the answer is that pretty much everything is a matter of interpretation. It's just as real an effect as everything else - but other people's different interpretations are just as legitimate.

Can you help with the other part of my question - what happens to a long object as it passes the return point and it has one clock running fast and the other more slowly as it passes?

 

[bhobba]

Can you help with the other part of my question - what happens to a long object as it passes the return point and it has one clock running fast and the other more slowly as it passes?

I don't know the detail of your query, but generally in SR acceleration is handled by analyzing it from an inertial frame it is accelerating relative to, and during small time intervals breaking the acceleration into regions of constant velocity so SR can be applied.

It sounds like a variant of the pole in the barn so called 'paradox' :
http://math.ucr.edu/home/baez/physics/Relativity/SR/barn_pole.html

I personally suggest you get a good book on Special Relativity - I like Rindler:
https://www.amazon.com/dp/0198539525/?tag=pfamazon01-20

Thanks
Bill

 

[SiennaTheGr8]

I would also caution that words like "look," "appear," "seem," and "observe" can be misleading, especially if they're used inconsistently.

In my comment about the "rear clock ahead" business, where I mentioned that for the rocket-twin it's as if the Earth-twin suddenly "jump ahead" very far into the future, it's not a question of what the rocket-twin SEES visually. Some of the comments in this thread have involved an observer using a telescope to physically observe a distant clock (where you have to factor in the time it takes the light to arrive). But that's not what I was talking about.

In the traditional twin-paradox scenario, there are three inertial reference frames to consider: Frame A, the rest frame that the Earth shares with the destination planet; Frame B, the rocket's outbound frame; and Frame C, the rocket's inbound frame.

Since the Earth and destination planet share a rest frame (Frame A), we can say that there's a clock on Earth and a clock on the destination planet that are synchronized in their shared rest frame.

But what do we mean when we say that the Frame-A clocks aren't synchronized in Frames B and C?

Imagine that in addition to the outbound rocket-twin, there's a second comoving Frame-B dweller who's headed toward Earth while the rocket-twin is headed toward the destination planet. Because they share a rest frame, they agree that their clocks are synchronized (in the same way that the aforementioned Frame-A clocks are synchronized in Frame A). Let's say that they're separated by just the right distance so that they arrive at their destinations simultaneously (in Frame B). At this shared Frame-B moment of arrival, the outbound rocket-twin records the reading on the destination-planet clock, and the other Frame-B dweller records the reading on the Earth clock. (Note that these measurements are made locally.) When they compare their results, they find that the Earth clock's reading was X years behind the destination-planet clock's reading. (The destination-planet clock was the "rear clock," and it's "rear clock ahead.")

The Frame-C situation is the reverse: a second Frame-C dweller locally records the reading on the Earth clock upon departure, and simultaneously (in Frame C) the inbound rocket-twin starts the return trip and locally records the reading on the destination-planet clock. When the Frame-C dwellers compare their results, they find that the Earth clock's reading was X years AHEAD of the destination-planet clock's reading, because now the Earth clock was the "rear clock."

By time dilation, the Earth does "age slowly" in both Frames B and C, but the Earth's age in Frame B at the end of the outbound trip is NOT the Earth's age in Frame C at the start of the inbound trip. For the rocket-twin, it's as if the Earth has suddenly aged by 2X years.

 

[Ibix]

Can you help with the other part of my question - what happens to a long object as it passes the return point and it has one clock running fast and the other more slowly as it passes?

I don't understand the question, I'm afraid. Are you asking what happens to a long object that moves with the traveling twin outbound, but doesn't turn round? Nothing happens to it - as I explained above, all of this simultaneity stuff is one or other twin interpreting their sensor readings. If you want a completely consistent interpretation for the traveling twin at turnaround you need to use a non-inertial frame. My favourite is radar coordinates - see https://arxiv.org/abs/gr-qc/0104077

 

[JulianM]

I don't understand the question, I'm afraid. Are you asking what happens to a long object that moves with the traveling twin outbound, but doesn't turn round? Nothing happens to it - as I explained above, all of this simultaneity stuff is one or other twin interpreting their sensor readings. If you want a completely consistent interpretation for the traveling twin at turnaround you need to use a non-inertial frame. My favourite is radar coordinates - see https://arxiv.org/abs/gr-qc/0104077

No, I was trying to clarify the point about the clocks going slower as the object moves away and then faster when it comes back.

Imagine that as it returns it passes the stay-at-home twin and the traveling twin is on a reasonably long object. At the point that it comes past Iwithout stopping) the front of the object is moving away from the stay-at-home and the reasr is coming towards him.
This would seem to result in a starnge situation, which I don't understand, of the clocks, on a presumably rigid object, appearing (or in actuality?) running at different speeds according to the stay-at-home (though presumably not for the traveller?)

The purpose of my question was to better understand post #45 which describes traveling away, changing direction and then coming back. I am not clear on whether just velocity, or direction causes this.

 

[bhobba]

But what do we mean when we say that the Frame-A clocks aren't synchronized in Frames B and C?

Frame A, B and C, - forget it.

We have two frames - some inertial frame the rocket takes off from and the rocket frame. We sync the clocks before the rocket takes off - for definiteness we use slow transport ie bring the rocket ship clock next to the inertial frame clock, sync them, then slow transport it to the rocket ship. They are now synced and in the same frame. So acceleration does not affect the clocks we will use atomic clocks. Now the rocket takes off. It's accelerated, so by the definition of an inertial frame as I previously explained is not inertial - since you can't use SR in non inertial frames you must do the analysis from the inertial frame. But you are then faced with the issue the rocket not being inertial how do you apply SR to it. Simple - you approximate the non inertial rocket by a series of constant velocities of short duration. You can use SR during those short durations since its going at constant velocity. Now to the actual analysis. You use world lines as the link I gave details. To get the time in each frame you simply integrate along the world line. In the accelerated world line in the rocket you have this dτ = √1-v^2 dt where dτ is the time change in the rocket clock and dt is the time change in the inertial frame clock (you can take the very small time change as the time increments you divide the acceleration into to apply SR). In the inertial frame dτ is the time change on its clock. You integrate both to get the change in time in each frame. dτ is prety easy in the inertial frame to get the difference τ. But in the rocket ship you have √1-v^2 in front of it which lies between 0 and 1. It can't always be 1 or no acceleration will occur. So when integrated you get a time difference less than the inertial frame ie less than τ.

Its not hard. Some here are way over complicating it.

Thanks
Bill

 

[Ibix]

No, I was trying to clarify the point about the clocks going slower as the object moves away and then faster when it comes back.

Right. The clocks run at the same speed, which is not the same speed as the stay-at-home's clocks. However, they are not synchronised correctly according to the stay-at-home although they are according to the traveling twin. "Leading clocks lag" doesn’t mean that leading clocks run more slowly, just that they were set to a time earlier than clocks behind them, according to a frame where they are moving.

What you actually see depends on the Doppler shift. Clocks coming towards you appear to run fast because each successive tick happens closer to you, so there's less lag and the ticks arrive closer together. And the reverse when they move away. As Sienna pointed out, people do not use "see" consistently and sometimes mean what you actually see (Doppler shift) or how you interpret it (time dilation and a leading-clocks-lag simultaneity change).

 

[bhobba]

No, I was trying to clarify the point about the clocks going slower as the object moves away and then faster when it comes back.

During an infinitesimal time interval the rocket clock is always running either slower or the same rate. It can't run at the same rate for the entire journey otherwise it would not move at all - little alone accelerate. When you add up the infinitesimal rates in each frame (called integration) since at some instants during the journey the rate of the rocket clock is slower it must be less than the stay at home clock. See that v^2 in the equation I wrote - that means direction is irrelevant.

Again its not hard - you just need to look at it correctly.

This - what will it look like if you observe it is a distraction. Understand what I said before thinking about it. IBIX is correct - but please don't try to understand it until you understand what I said or you will likely get confused.

Thanks
Bill

 

[SiennaTheGr8]

Frame A, B and C, - forget it.

We have two frames - some inertial frame the rocket takes off from and the rocket frame. We sync the clocks before the rocket takes off - for definiteness we use slow transport ie bring the rocket ship clock next to the inertial frame clock, sync them, then slow transport it to the rocket ship. They are now synced and in the same frame. So acceleration does not affect the clocks we will use atomic clocks. Now the rocket takes off. It's accelerated, so by the definition of an inertial frame as I previously explained is not inertial - since you can't use SR in non inertial frames you must do the analysis from the inertial frame. But you are then faced with the issue the rocket not being inertial how do you apply SR to it. Simple - you approximate the non inertial rocket by a series of constant velocities of short duration. You can use SR during those short durations since its going at constant velocity. Now to the actual analysis. You use world lines as the link I gave details. To get the time in each frame you simply integrate along the world line. In the accelerated world line in the rocket you have this dτ = √1-v^2 dt where dτ is the time change in the rocket clock and dt is the time change in the inertial frame clock (you can take the very small time change as the time increments you divide the acceleration into to apply SR). In the inertial frame dτ is the time change on its clock. You integrate both to get the change in time in each frame. dτ is prety easy in the inertial frame to get the difference τ. But in the rocket ship you have √1-v^2 in front of it which lies between 0 and 1. It can't always be 1 or no acceleration will occur. So when integrated you get a time difference less than the inertial frame ie less than τ.

Its not hard. Some here are way over complicating it.

Thanks
Bill

Overcomplicated? I don't think three inertial frames is even complicated. If anything it's an oversimplification, since the rocket twin switches directions without undergoing acceleration (physically impossible). As I tried to show in my post above, the "rear clock ahead" effect is key to understanding this three-frame approach. The math is straightforward.

Of course, your "incremental acceleration" approach works too, and if I remember correctly Taylor and Wheeler use it in Spacetime Physics.

Also, SR can handle accelerated motion (and accelerated frames) just fine.

 

[bhobba]

If anything it's an oversimplification

Two frames vs three frames? To each their own I suppose.

And didn't I just explain it handles accelerated frames just fine? - but you must do it the way I described, or something similar. SR works only in inertial frames. You have to use various 'tricks' for other frames. They are not hard - but are required. Its in the very derivation of the Lorentz transformations eg:
http://www2.physics.umd.edu/~yakovenk/teaching/Lorentz.pdf

Thanks
Bill

 

[SiennaTheGr8]

Two frames vs three frames? To each their own I suppose.

And didn't I just explain it handles accelerated frames just fine? - but you must do it the way I described, or something similar. SR works only in inertial frames. You have to use various 'tricks' for other frames. They are not hard - but are required. Its in the very derivation of the Lorentz transformations eg:
http://www2.physics.umd.edu/~yakovenk/teaching/Lorentz.pdf

Thanks
Bill

Well, you said:

... since you can't use SR in non inertial frames you must do the analysis from the inertial frame. But you are then faced with the issue the rocket not being inertial how do you apply SR to it. Simple - you approximate the non inertial rocket by a series of constant velocities of short duration. You can use SR during those short durations since its going at constant velocity. ...

(which did seem somewhat contradictory to what you said next about integrating!).

 

[Janus]

When you say LOOKS do you mean it's not real?

First you have to define what you mean by "LOOKS".

In your post above, you ask about a clock that runs fast when approaching and slow when receding. In this case, LOOKS means "what you see visually" and involves Doppler shift. You get a Doppler shift whether you include Relativistic effects or not. You see a clock coming towards you run fast, because the distance between you and it is constantly decreasing and light take less and less time to cross the distance. This causes the light and information about events it carries to "scrunch up" If the clock is receding the distance is constantly increasing, the light takes longer and longer the cross the distance, and things are stretched out.

If we account for this time lag, we can get a better idea of what that clock is doing compared to our own. When we do this, then we find that whether the clock is receding or approaching, it runs slow. A lot of the time you will hear it said that the clock "appears" to slow. This is because from that clock's perspective, it is your clock that it the one that runs slow and neither clock runs slower than the other in an absolute sense. Here, "appears" does not mean "what we see with our eyes", but what we determine as to what the clock is doing.

If we go back to the post by SiennaTheGr8 you quoted, they were talking about "appears" rather than "LOOK"S. In this case, when the Rocket twin changes from traveling away from to traveling towards, he does visually see the Earth clock go from running slow to running fast, but he will determine that it was running slow in both cases.
But what SiennaTheGr8 was referring to is what happens to the Earth clock at that instant he changes direction. If we assume that he changes direction instantaneously, then the light he is getting from the Earth is the same both before and after the change, and he visually sees no change in the Earth's clock's reading. What does change is what time the Earth Clock "appears" to have (the time on the Earth clock "Now" after he accounts for the time it took the light to reach him. What happens is that the Earth clock goes from being lagging behind his clock to leading it by some time. the time he considers it to be on Earth "right now" changes even though the time he "sees" on the Earth clock doesn't change.

 

[robphy]

Can you help with the other part of my question - what happens to a long object as it passes the return point and it has one clock running fast and the other more slowly as it passes?

I don't understand the question, I'm afraid. Are you asking what happens to a long object that moves with the traveling twin outbound, but doesn't turn round? Nothing happens to it - as I explained above, all of this simultaneity stuff is one or other twin interpreting their sensor readings. If you want a completely consistent interpretation for the traveling twin at turnaround you need to use a non-inertial frame. My favourite is radar coordinates - see https://arxiv.org/abs/gr-qc/0104077

No, I was trying to clarify the point about the clocks going slower as the object moves away and then faster when it comes back.

Imagine that as it returns it passes the stay-at-home twin and the traveling twin is on a reasonably long object. At the point that it comes past without stopping) the front of the object is moving away from the stay-at-home and the rear is coming towards him.
This would seem to result in a strange situation, which I don't understand, of the clocks, on a presumably rigid object, appearing (or in actuality?) running at different speeds according to the stay-at-home (though presumably not for the traveller?)

The purpose of my question was to better understand post #45 which describes traveling away, changing direction and then coming back. I am not clear on whether just velocity, or direction causes this.

From my reading of your original question and this bolded part of your reply to Ibix,
I think this situation (of an extended object passing the home frame) will address your question.
I've drawn a spacetime diagram on rotated graph paper.

Alice is at rest.
Bob, moving with velocity (6/10)c=(3/5)c. is traveling with a "co-moving inertial" ruler whose proper length is 10.
The Back of the ruler is in blue.
The ruler can be thought of as a fleet of inertial clocks traveling with Bob... just focus on the front (where Bob is) and the Back.
The clocks on the ruler are synchronized in Bob's frame.
At event O, Alice and Bob meet. For simplicity, they have pre-arranged to have their clocks set to read "0" at this event.DOPPLER:

• Here are Alice's visual observations.
  At event O (when Alice and Bob meet), Alice sees the image of "-10" on the Back clock and the image of "0" on Bob's clock.
  
  When Alice's clock reads 6, she sees 2 on the Back clock and 3 on Bob's clock.
  • The Back clock approaching Alice had an elapsed time of 12 between her readings...
    that is, Alice watched 12 hours of Back's tv-programming in 6 hours...
    this factor of 12/6 is the Doppler factor relating frequencies ("blueshift for approaching")
  • Bob's clock receding from Alice had an elapsed time of 3 between her readings...
    that is, Alice watched 3 hours of Bob's tv-programming in 6 hours...
    this factor of 3/6 is the Doppler factor relating frequencies ("redshift for receding")
  • This factor of 2 and its reciprocal values correspond to v=(3/5)c.
• Between Alice's clock readings at 6 and 12, we highlight the 3-tick intervals from the Back clock and from Bob's clock.
  
• You can draw your own lightlike lines to see how each clock sees the images of each other's clock.
  For instance, how does Bob see the Back clock? How does the Back clock see Bob's clock?

TIME-DILATION:

• In Alice's frame of reference, her time marches on with her lines-of-simultaneity (Minkowski-perpendicular to her worldline).
  • Alice says "the event when her clock reads -5" is simultaneous with both
    • "the event when Bob's clock reads -4"
    • "the event when the Back clock reads 2"
  • Alice says "the event when her clock reads 0" is simultaneous with both
    • "the event when Bob's clock reads 0"
    • "the event when the Back clock reads 6"

• Alice says "the event when her clock reads 5" is simultaneous with both
  • "the event when Bob's clock reads 4"
  • "the event when the Back clock reads 10"

• Alice says when Bob's clock elapses 4 ticks, her clock has elapsed 5 ticks.
  Alice says when the Back clock elapses 4 ticks, her clock has elapsed 5 ticks.
  And this persists before and after the ruler passes Alice.
  This ratio 5/4 is the time-dilation factor corresponding to v=(3/5)c.
  Note that the time-dilation factor \gamma=\frac{1}{\sqrt{1-v^2}} is an even function of velocity...
  so it depends on the relative-speed, not the direction (approaching vs receding).

If you analyze the situation from Bob's frame of reference with his lines-of-simultaneity (Minkowski-perpendicular to his worldline),
he will come to the same conclusion:
Bob says when Alice's clock elapses 4 ticks, his clock has elapsed 5 ticks.
And this persists before and after the ruler passes Alice (or Alice passes the ruler).
This ratio 5/4 is the same time-dilation factor corresponding to v=(3/5)c.

​

 

[PeterDonis]

Thead closed for moderation.

Edit: A number of off topic posts have been deleted. The original question has been sufficiently addressed, and the thread will remain closed.