- 24,488
- 15,056
- TL;DR Summary
- Twin paradox for two twins freely falling around a spherically symmetric non-rotating star (Schwarzschild spacetime)
Here I consider the twin paradox for two observers moving in the Schwarzschild spacetime, i.e., the spacetime where one has one radially symmetric non-rotating star, leading to the invariant line element (written in the usual Schwarzschild coordinates)
$$\mathrm{d} s^2=\left (1-\frac{R}{r} \right) \mathrm{d} t^2 - \left (\frac{1}{1-R/r} \mathrm{d}r^2 + r^2 \mathrm{d} \vartheta^2 + r^2 \sin^2 \vartheta \mathrm{d} \varphi^2\right).$$
I use units with ##c=1##. The Schwarzschild radius ##R=2 G M##, where ##G## is Newton's gravitational constant and ##M## the mass of the star.
Now we consider two twins, who fall freely around this star. Twin 1 is going along a circle ##r=r_1 \text{const}## and the other, twin 2, starts with a radial velocity such that he moves along a radius from ##r=r_1## to a radius ##r_2##, where ##r_2## is chosen such that the twins meet again at the same event after twin 1 has moved once around the star.
We need the geodesics of this space time, and it's most simple to use the "square form" of the Hamilton principle of least action, where
$$L=-\frac{1}{2} \left (\frac{\mathrm{d} s}{\mathrm{d} \lambda} \right)=-\frac{1}{2} g_{\mu \nu} \dot{x}^{\mu} \dot{x}^{\nu}.$$
This has the advantage that the worldline parameter, ##\lambda##, is automatically an affine parameter, because
$$p_{\mu} \dot{x}^{\mu}-L=\text{const}, \quad p_{\mu} = \frac{\partial L}{\partial \dot{x}^{\mu}},$$
because the Lagrangian doesn't depend explicitly on ##\Lambda##. Further it's a 2nd-rank homogeneous function in the ##\dot{x}^{\mu}## and thus
$$p_{\mu} \dot{x}^{\mu}-L=L=\text{const}.$$
Thus we can choose ##\lambda=\tau##, the proper time of any observer in free fall.
The Lagrangian is obviously symmetric under arbitrary rotations around the star and thus angular momentum is conserved. This means the geodesics are all in a plane perpendicular to angular momentum, and it's convenient to choose the coordinate system such that this plane is determined by ##\vartheta=\pi/2=\text{const}##. For such plane orbits the Lagrangian simpifies to
$$L=\frac{1}{2} \left [\frac{1}{1-R/r} \dot{r}^2 + r^2 \dot{\varphi}^2 - \left (1-\frac{R}{r} \right) \dot{t}^2 \right ].$$
Now both ##t## and ##\varphi## are cylcic, i.e., the corresponding canonical momenta are conserved,
$$p_t=-E=-\dot{t} \left (1-\frac{R}{r} \right)=\text{const} \qquad (*)$$
and
$$p_{\varphi}=h=r^2 \dot{\varphi}=\text{const}.$$
Finally we have the condition ##\lambda=\tau## for the world-line parameter,
$$\left (1-\frac{R}{r} \right) \dot{t}^2 - \left (\frac{1}{1-R/r} \dot{r}^2 + r^2 \dot{\varphi}^2 \right)=1.$$
Plugging in the conservation laws leads after some algebra to
$$\dot{r}^2=E^2- \left (1+\frac{R}{r} \right) \left (1+\frac{h^2}{r^2} \right). \qquad (1)$$
Deriving this equation wrt. ##\lambda=\tau## leads to
$$\ddot{r}=-\partial_r V_{\text{eff}}, \quad V_{\text{eff}} = \left (1-\frac{R}{r} \right) \left (1+\frac{h^2}{r^2} \right).$$
Now we want to get the solution for twin ##1## moving along a circle ##r=r_1=\text{const}##. For this you need the minimum of the potential, which leads to the condition
$$\partial_r V_{\text{eff}}|_{r=r_1}=0 \; \Rightarrow \; h^2(2r_1-3R)-r_1^2 R=0,$$
which determines
$$h^2=\frac{R r_1^2}{2r_1-3R}. \qquad (2)$$
So we must have ##r_1>3R/2##. For the angular velocity ##\dot{\varphi}=\mathrm{d}_{\tau} \varphi## we get
$$h=r_1^2 \dot{\varphi} \; \Rightarrow \; \dot{\varphi}=\sqrt{\frac{GM}{r_1^3}},$$
and thus the period of the twin 1's orbit is given by
$$\tau_1=2 \pi r_1 \sqrt{\frac{2r_1-3R}{R}}.$$
The corresponding coordinate time is
$$t_1=\frac{E \tau_1}{1-R/r_1}.$$
From (1) we get with ##\dot{r}=0## and using (2)
$$E^2=2 \left (1-\frac{R}{r_1} \right ) \frac{r_1-R}{2r_1-3R}.$$
And thus for the coordinate time after one orbit of twin 1
$$t_1=2 \pi \sqrt{\frac{2 r_1^3}{R}}.$$
For twin 2 we assume that he starts from ##r=r_1##, ##\vartheta=\pi/2## radially out moving to ##r=r_2## and then falling back to ##r=r_1##. It's ##\varphi=\text{const}## and thus ##h=0##. From (1) we get
$$\dot{r}^2=E^2-1+\frac{R}{r}. \qquad (3)$$
To have the turning point at ##r=r_2## we must have ##\dot{r}=0## such that
$$E^2=1-\frac{R}{r_2}.$$
(3) is easily solved by "separation of variables"
$$\mathrm{d} \tau = \pm \frac{\mathrm{d} r}{\sqrt{R(1/r-1/r_2)}}. \qquad (4)$$
To get the proper time ##\tau_2## at which twin 2 is back at his starting point ##r=r_1## we note that this is twice the proper time he needs to move from ##r_1## to ##r_2##, and there we have to choose the positive sign in (4). So we find
$$\tau_2=2 \int_{r_1}^{r_2} \mathrm{d} r \frac{1}{\sqrt{R(1/r-1/r_2)}} = 2 \frac{r_2-r_1+r_2 \sqrt{r_2/r_1-1} \arctan(\sqrt{r_2/r_1-1}}{\sqrt{R(1/r_1-1/r_2)}}.$$
To determine ##r_2## from the condition that twin 2 should meet twin 1 again after the latter has made one orbit around the star we also need the coordinate time ##t_2## when twin 2 is again at ##r=r_1##. To that end it's most simple to derive an equation for ##r(t)##. With (3) and (*) we get
$$\frac{\mathrm{d} t}{\mathrm{d} r}=\frac{\dot{t}}{\dot{r}}=\pm \frac{r}{r-R} \sqrt{\frac{(r2-R)r}{(r2-r)R}}.$$
For the total time we just need to take twice the integral for ##r \in \{r_1,r_2\}## with the positive sign of the square root:
$$t_2=2 \left [\pi \left (\sqrt{R(r_2-R)}+\frac{r_2}{2} \sqrt{\frac{r_2-R}{R}} \right )+ \sqrt{\frac{r_1(r_2-r_1)(R_2-R)}{R}}-(2R+r_2) \sqrt{\frac{r_2-R}{R}} \arcsin \left (\sqrt{\frac{r_1}{r_2}} \right) + R \ln \left ( \frac{R(r_2-r_1)}{\sqrt{R r_1 (r_2-R)(r_2-r_1)}}-R(r_2-r_1) \right) + R \ln \left (1+\sqrt{\frac{r_1(r_2-R)}{R(r_2-r_1)}} \right )\right].$$
To resolve the equation ##t_1=t_2## one needs of course numerics. The result can be seen in the following plot
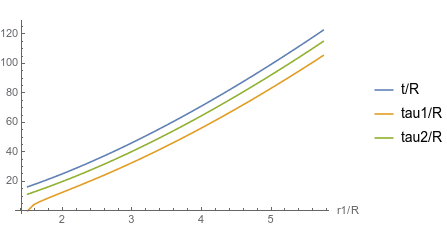
As one can see twin 1 on his circular orbit stays younger than twin 2, who is thrown radially up and falling down again.
Since both twins are freely falling and thus their local frames are always inertial (in the sense of GR) this is a purely gravitational time delay. The coordinate time is of course always the largest time meausure. It's the proper time for an observer at ##r \rightarrow \infty## with fixed spatial coordinates ##(r,\vartheta,\varphi)##.
The calculation was done using Mathematica 12.0.
$$\mathrm{d} s^2=\left (1-\frac{R}{r} \right) \mathrm{d} t^2 - \left (\frac{1}{1-R/r} \mathrm{d}r^2 + r^2 \mathrm{d} \vartheta^2 + r^2 \sin^2 \vartheta \mathrm{d} \varphi^2\right).$$
I use units with ##c=1##. The Schwarzschild radius ##R=2 G M##, where ##G## is Newton's gravitational constant and ##M## the mass of the star.
Now we consider two twins, who fall freely around this star. Twin 1 is going along a circle ##r=r_1 \text{const}## and the other, twin 2, starts with a radial velocity such that he moves along a radius from ##r=r_1## to a radius ##r_2##, where ##r_2## is chosen such that the twins meet again at the same event after twin 1 has moved once around the star.
We need the geodesics of this space time, and it's most simple to use the "square form" of the Hamilton principle of least action, where
$$L=-\frac{1}{2} \left (\frac{\mathrm{d} s}{\mathrm{d} \lambda} \right)=-\frac{1}{2} g_{\mu \nu} \dot{x}^{\mu} \dot{x}^{\nu}.$$
This has the advantage that the worldline parameter, ##\lambda##, is automatically an affine parameter, because
$$p_{\mu} \dot{x}^{\mu}-L=\text{const}, \quad p_{\mu} = \frac{\partial L}{\partial \dot{x}^{\mu}},$$
because the Lagrangian doesn't depend explicitly on ##\Lambda##. Further it's a 2nd-rank homogeneous function in the ##\dot{x}^{\mu}## and thus
$$p_{\mu} \dot{x}^{\mu}-L=L=\text{const}.$$
Thus we can choose ##\lambda=\tau##, the proper time of any observer in free fall.
The Lagrangian is obviously symmetric under arbitrary rotations around the star and thus angular momentum is conserved. This means the geodesics are all in a plane perpendicular to angular momentum, and it's convenient to choose the coordinate system such that this plane is determined by ##\vartheta=\pi/2=\text{const}##. For such plane orbits the Lagrangian simpifies to
$$L=\frac{1}{2} \left [\frac{1}{1-R/r} \dot{r}^2 + r^2 \dot{\varphi}^2 - \left (1-\frac{R}{r} \right) \dot{t}^2 \right ].$$
Now both ##t## and ##\varphi## are cylcic, i.e., the corresponding canonical momenta are conserved,
$$p_t=-E=-\dot{t} \left (1-\frac{R}{r} \right)=\text{const} \qquad (*)$$
and
$$p_{\varphi}=h=r^2 \dot{\varphi}=\text{const}.$$
Finally we have the condition ##\lambda=\tau## for the world-line parameter,
$$\left (1-\frac{R}{r} \right) \dot{t}^2 - \left (\frac{1}{1-R/r} \dot{r}^2 + r^2 \dot{\varphi}^2 \right)=1.$$
Plugging in the conservation laws leads after some algebra to
$$\dot{r}^2=E^2- \left (1+\frac{R}{r} \right) \left (1+\frac{h^2}{r^2} \right). \qquad (1)$$
Deriving this equation wrt. ##\lambda=\tau## leads to
$$\ddot{r}=-\partial_r V_{\text{eff}}, \quad V_{\text{eff}} = \left (1-\frac{R}{r} \right) \left (1+\frac{h^2}{r^2} \right).$$
Now we want to get the solution for twin ##1## moving along a circle ##r=r_1=\text{const}##. For this you need the minimum of the potential, which leads to the condition
$$\partial_r V_{\text{eff}}|_{r=r_1}=0 \; \Rightarrow \; h^2(2r_1-3R)-r_1^2 R=0,$$
which determines
$$h^2=\frac{R r_1^2}{2r_1-3R}. \qquad (2)$$
So we must have ##r_1>3R/2##. For the angular velocity ##\dot{\varphi}=\mathrm{d}_{\tau} \varphi## we get
$$h=r_1^2 \dot{\varphi} \; \Rightarrow \; \dot{\varphi}=\sqrt{\frac{GM}{r_1^3}},$$
and thus the period of the twin 1's orbit is given by
$$\tau_1=2 \pi r_1 \sqrt{\frac{2r_1-3R}{R}}.$$
The corresponding coordinate time is
$$t_1=\frac{E \tau_1}{1-R/r_1}.$$
From (1) we get with ##\dot{r}=0## and using (2)
$$E^2=2 \left (1-\frac{R}{r_1} \right ) \frac{r_1-R}{2r_1-3R}.$$
And thus for the coordinate time after one orbit of twin 1
$$t_1=2 \pi \sqrt{\frac{2 r_1^3}{R}}.$$
For twin 2 we assume that he starts from ##r=r_1##, ##\vartheta=\pi/2## radially out moving to ##r=r_2## and then falling back to ##r=r_1##. It's ##\varphi=\text{const}## and thus ##h=0##. From (1) we get
$$\dot{r}^2=E^2-1+\frac{R}{r}. \qquad (3)$$
To have the turning point at ##r=r_2## we must have ##\dot{r}=0## such that
$$E^2=1-\frac{R}{r_2}.$$
(3) is easily solved by "separation of variables"
$$\mathrm{d} \tau = \pm \frac{\mathrm{d} r}{\sqrt{R(1/r-1/r_2)}}. \qquad (4)$$
To get the proper time ##\tau_2## at which twin 2 is back at his starting point ##r=r_1## we note that this is twice the proper time he needs to move from ##r_1## to ##r_2##, and there we have to choose the positive sign in (4). So we find
$$\tau_2=2 \int_{r_1}^{r_2} \mathrm{d} r \frac{1}{\sqrt{R(1/r-1/r_2)}} = 2 \frac{r_2-r_1+r_2 \sqrt{r_2/r_1-1} \arctan(\sqrt{r_2/r_1-1}}{\sqrt{R(1/r_1-1/r_2)}}.$$
To determine ##r_2## from the condition that twin 2 should meet twin 1 again after the latter has made one orbit around the star we also need the coordinate time ##t_2## when twin 2 is again at ##r=r_1##. To that end it's most simple to derive an equation for ##r(t)##. With (3) and (*) we get
$$\frac{\mathrm{d} t}{\mathrm{d} r}=\frac{\dot{t}}{\dot{r}}=\pm \frac{r}{r-R} \sqrt{\frac{(r2-R)r}{(r2-r)R}}.$$
For the total time we just need to take twice the integral for ##r \in \{r_1,r_2\}## with the positive sign of the square root:
$$t_2=2 \left [\pi \left (\sqrt{R(r_2-R)}+\frac{r_2}{2} \sqrt{\frac{r_2-R}{R}} \right )+ \sqrt{\frac{r_1(r_2-r_1)(R_2-R)}{R}}-(2R+r_2) \sqrt{\frac{r_2-R}{R}} \arcsin \left (\sqrt{\frac{r_1}{r_2}} \right) + R \ln \left ( \frac{R(r_2-r_1)}{\sqrt{R r_1 (r_2-R)(r_2-r_1)}}-R(r_2-r_1) \right) + R \ln \left (1+\sqrt{\frac{r_1(r_2-R)}{R(r_2-r_1)}} \right )\right].$$
To resolve the equation ##t_1=t_2## one needs of course numerics. The result can be seen in the following plot
As one can see twin 1 on his circular orbit stays younger than twin 2, who is thrown radially up and falling down again.
Since both twins are freely falling and thus their local frames are always inertial (in the sense of GR) this is a purely gravitational time delay. The coordinate time is of course always the largest time meausure. It's the proper time for an observer at ##r \rightarrow \infty## with fixed spatial coordinates ##(r,\vartheta,\varphi)##.
The calculation was done using Mathematica 12.0.