Considering the case ##V_0 = 0 ##.
Assuming potential energy is zero at the initial (and final) point, and ##y## growing downward, conservation of energy yields $$ v = \sqrt {2gy} .$$ The horizontal component of velocity is $$v_x = v \cos n,$$ where ##n## is the angle of the velocity with the horizontal, so $$ \tan n = y'(x), $$ giving $$v_x = {v \over \sqrt {1 + (y')^2}} $$ Assuming further ##x = 0## at the initial point and ##x = a## at the final point, the total time of travel is $$ T= \int\limits_0^a {dx \over v_x} = {1 \over \sqrt {2g}} \int\limits_0^a \sqrt {1 + (y')^2 \over y} dx $$ The integrand does not depend on ##x##, so the Beltrami identity can be employed: $$ \sqrt {1 + (y')^2 \over y} - \frac {y'} {\sqrt y} \frac {y'} {\sqrt {1 + (y')^2} } = {1 \over \sqrt y \sqrt {1 + (y')^2} } = C ,$$ so $$ y' = \sqrt {\frac D y - 1}, $$ which is the differential equation of the inverted cycloid generated by a circle of radius ##D## (c.f.
http://en.wikipedia.org/wiki/Brachistochrone_problem). Thus, $$ T = \sqrt {D \over 2 g} \int\limits_0^a {dx \over y} .$$ A canonical parametrization of the cycloid is $$ x = \frac D 2 (u - \sin u) \\ y = \frac D 2 (1 - \cos u) $$ (c.f.
http://en.wikipedia.org/wiki/Cycloid#Area), where ##u## is the angle of rotation of the generating circle. In this problem one full rotation ##u = 2 \pi ## must correspond to horizontal displacement ##a##, so $$ D = {a \over \pi} ,$$ and the total time integral becomes $$ T = \sqrt {a \over 2\pi g} \int \limits_0^{2 \pi} {1 - \cos u \over 1 - \cos u } du = \sqrt {2\pi a \over g} .$$ Thus the minimal time of motion for a particle starting from rest and reaching the same height at a given distance, where minimization is over the set of
arbitrary smooth curves, is finite and is realized when the curve is the inverted cycloid specified above.
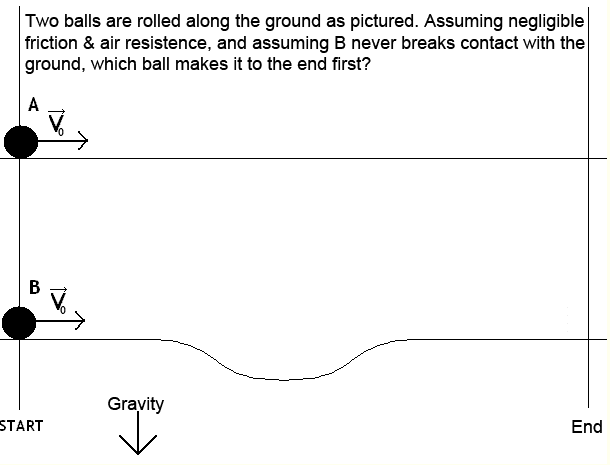
A question remains, is such a motion realizable when the particle slides freely "on top" of the curve?
$$ v = \sqrt {\dot x^2 + \dot y^2} = \sqrt {1 + (y')^2 } \dot x = \sqrt {D \over y} \dot x= \sqrt {2 g y }, $$ hence $$ \dot x = \sqrt {2g \over D} y, $$ and, using the parametric equations above, $$ (1 - \cos u) \dot u = \sqrt {2g \over D} (1 - \cos u), $$ giving $$ u(t) = \sqrt {2 \pi g \over a} t. $$
Acceleration vector: $$ \ddot x = g \sin \sqrt {2 \pi g \over a} t \\ \ddot y = g \cos \sqrt {2 \pi g \over a} t. $$ The force gravity is ##(0, mg)##, hence the normal force is $$ N_x = mg \sin \sqrt {2 \pi g \over a} t \\ N_y = mg \cos \sqrt {2 \pi g \over a} t - mg. $$ The vertical component is everywhere non-positive, i.e, directed upward, so a cycloidal track does not "pull" the particle downward; the horizontal component is positive during the descent, and negative during the ascent, again as is to be expect from a track that can be "freely slidden upon" by a particle, which I think settles the issue completely for the case ##V_0 = 0 ##.
Turning to ##V_0 \ne 0 ## now. As I said earlier, by introducing a reference frame moving uniformly at ##V_0##, the problem is reduced to the one just dealt with above. To which haruspex (and possibly others) objected, reasoning that an inverted cycloid cannot possibly be a path "freely slidden upon" by a particle whose initial horizontal velocity is not zero, because such a path is vertical initially. That argument is flawed, however, because the inverted cycloid is the minimal time path in the initially comoving frame; in the lab frame where ##V_0 \ne 0##, the minimal time path is the trajectory of the particle following a cycloidal path in the initially comoving frame; that path is not a cycloid per se. Moreover, the width of the dip in the lab frame is not distance ##a## in the initially comoving frame.
Let the width of the dip be ##A##. During time ##T##, the initially comoving frame will cover ##V_0 T##; in the initially comoving frame, the particle will cover ##a##. So, $$ A = V_0 T + a = V_0 T + {g \over 2\pi} T^2 , $$ yielding $$ T = {\pi \over g } \left( -V_0 + \sqrt {V_0^2 + {2 A g \over \pi}} \right) .$$
I hope there are no mistakes in the above, but any corrections are welcome.