Two battery circuit charging one capacitor

[dtecker]

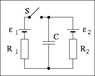
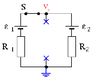
See attached photo for circuit diagram.

The switch S has been open for a long time. Determine the magnitude of the electric charge stored by the capacitor. Use the following data: C = 3.43 mF, ε1 = 11.0 V, ε2 = 31.9 V, R1 = 3.66 Ω, R2 = 5.04 Ω.
I understand how to determine the magnitude of charge with one battery and one capacitor using Q=VC.
Q=.109 C

However, I don't understand how to evaluate with this circuit setup.

Now the switch is closed, and you wait for a long time. How much electric charge does the capacitor store now?

I attempted to simply add the voltage of the two batteries together then used Q=VC but that isn't right because the current wouldn't flow that way from the 11V battery. The 31.9V battery would split its current between the capacitor and the wire to the other battery and resistor.

What approach do I need to take to calculate the charge on the capacitor with the switch closed?

Thanks

 

[gneill]

What approach do I need to take to calculate the charge on the capacitor with the switch closed?

Hi dtecker,

Welcome to Physics Forums!

A general approach for these types of problem is to "remove" the capacitor from the circuit and determine the potential across the terminals where it was connected:

After sufficient time, the current into or out of the capacitor will be zero (steady state reached), so that the potential across the capacitor must be equal to the potential that the surrounding circuit would "like" to impose across it. Find that potential and you can then determine the charge on the capacitor.