robot6
- 13
- 1
- Homework Statement
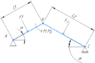
- I have a two beam problem, see illustration below. The problem requires a solution for the left beam and for the right beam.
- Relevant Equations
- ##\Sigma F_x = 0##
##\Sigma F_y = 0##
##\Sigma M = 0##
I've drastically simplified the problem for the sake of discussion. The problem is that I end up with six equations and seven unknowns. Let ##R_{AX}## (and similar) be the reaction force at the A node in the rightward direction on the page, and ##R_{AY}## (and similar) be the reaction force at the A node in the upward direction on the page. ##M## is an applied moment and ##M_B## is the reactive moment at node B.
For the left beam, I have:
##R_{AX}+R_{BX}+F_1\sin(\alpha) = 0##
##R_{AY}+R_{BY}-F_1\cos(\alpha) = 0##
##R_{AX}L_1\sin(\alpha)-R_{AY}L_1\cos{\alpha}+M+M_B=0##
For the right beam, I have:
##R_{BX}+R_{CX}-F_2\sin(\alpha)=0##
##R_{BY}+R_{CY}-F_2\cos(\alpha)=0##
##R_{CX}L_2\sin(\alpha)+R_{CY}L_2\cos{\alpha}+M_B=0##
So I have six equations and seven unknowns, namely, ##R_{AX}, R_{AY}, R_{BX}, R_{BY}, R_{CX}, R_{CY}, M_B##. What am I missing?
Thank you for your great kindness and answering.
For the left beam, I have:
##R_{AX}+R_{BX}+F_1\sin(\alpha) = 0##
##R_{AY}+R_{BY}-F_1\cos(\alpha) = 0##
##R_{AX}L_1\sin(\alpha)-R_{AY}L_1\cos{\alpha}+M+M_B=0##
For the right beam, I have:
##R_{BX}+R_{CX}-F_2\sin(\alpha)=0##
##R_{BY}+R_{CY}-F_2\cos(\alpha)=0##
##R_{CX}L_2\sin(\alpha)+R_{CY}L_2\cos{\alpha}+M_B=0##
So I have six equations and seven unknowns, namely, ##R_{AX}, R_{AY}, R_{BX}, R_{BY}, R_{CX}, R_{CY}, M_B##. What am I missing?
Thank you for your great kindness and answering.