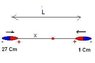
_Chemicals_ said:Homework Statement
THE ANSWER IS C
Homework Equations
None given. Pondering:
E=(1/(2(pi)εnaught))(σ/z^3)
p=qd
U=-p dotprod E
The Attempt at a Solution
We have attempted many variations of the above equations to try and find the answer. We are just seeking a point in the right direction as we are currently reviewing for a final. Any help is appreciated, thank you!
. You have two dipoles, one of magnitude p1=27 Cm, the other p2=1Cm at distance L from each other. What is their resultant field at distance x from the bigger one?
_Chemicals_ said:
Dipoles are formed when there is a separation of positive and negative charges within a molecule. This can occur due to differences in electronegativity between atoms or due to an external electric field.
The placement of two dipoles on an axis can result in the cancellation of the electric field at certain points. This occurs when the two dipoles are aligned in opposite directions and the electric field vectors cancel out.
Yes, there is a specific point where the electric field vanishes for two dipoles on an axis. This point is located on the axis between the two dipoles and is determined by the distance between the dipoles and their strengths.
The location of the point where the electric field vanishes for two dipoles on an axis is affected by the distance between the dipoles, the strengths of the dipoles, and the alignment of the dipoles. The closer the dipoles are to each other, the stronger the electric field at the point of cancellation.
If the dipoles on the axis have different strengths, the electric field at the point of cancellation will not completely vanish. Instead, it will be reduced in magnitude compared to the case where the dipoles have equal strengths. The electric field at this point is also influenced by the distance between the dipoles and their alignment.
