robtum
- 2
- 0
- Homework Statement
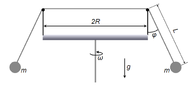
- Two masses m are attached to opposite ends of an ideal piece of string
(massless, flexible) that rests on two frictionless, massless pulleys. The pulleys are fixed
to a rotating platform. The masses are stable when the platform stands still (does not
rotate), and the string hangs vertically from the pulleys. The platform is then carefully
rotated about the axis in the middle, such that the two ends of the string both form the
same angle φ with respect to vertical.
[Numerical values: m = 0.5 kg; R = 0.3 m; L = 0.6 m; g = 9.8 m/s2]
(a) What is the tension in the string when the masses hang vertically, i.e. before the platform starts rotating?
(b) Find the angular velocity ω so that the angle φ = 60◦.
(c) What is the tension in the string given the conditions in (b)?
- Relevant Equations
- U = mgh
v = ωr
a = ω^2 r
K = 1/2 m v^2
I'm having some trouble figuring this problem out. I've found the tension in (a) but I don't know where to start with (b). I've found that the distance between one of the masses and the rotational axis on the picture is R+0.52 m and that the masses rise to a height of h = 0.3 m.
The moment of inertia for the platform isn't given, so I don't know how to figure out the angular velocity. I tried using conservation of energy, that is 1/2 m v^2 = 2mgh, and the formula v = ωr. I've also tried using the tension in the strings, so that ω = sqrt((T sin(φ))/(m(R+0.52))) where T is the tension in the string but that value of ω doesn't match up with the value I get using conservation of energy. Any ideas on what I've done wrong?
The moment of inertia for the platform isn't given, so I don't know how to figure out the angular velocity. I tried using conservation of energy, that is 1/2 m v^2 = 2mgh, and the formula v = ωr. I've also tried using the tension in the strings, so that ω = sqrt((T sin(φ))/(m(R+0.52))) where T is the tension in the string but that value of ω doesn't match up with the value I get using conservation of energy. Any ideas on what I've done wrong?